Предмет: Математика,
автор: imadridist6
Вычислить двойной интеграл по области D, ограниченной указанными линиями.
ФОТО ПРИКРЕПИЛ
Приложения:
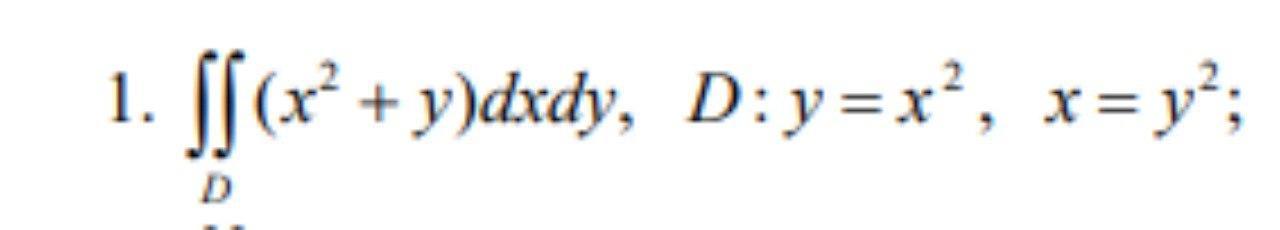
Ответы
Автор ответа:
0
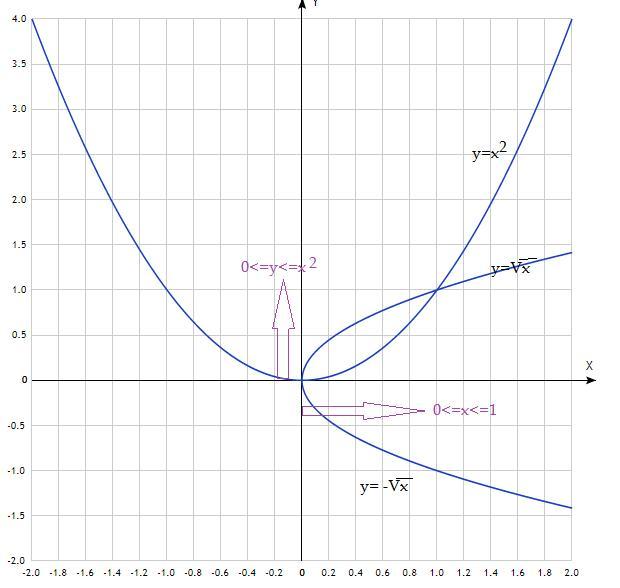
Расставим пределы интегрирования и перейдем к повторным интегралам.
см.Рисунок
Приложения:
imadridist6:
Помогите еще с таким если не сложно Используя тройной интеграл, вычислить объем тела 1) z²=4-x , x²+y²=4x
Похожие вопросы
Предмет: Русский язык,
автор: Кекбывает
Предмет: Английский язык,
автор: Бентос
Предмет: Английский язык,
автор: ptanya04
Предмет: Русский язык,
автор: elena2566
Предмет: Алгебра,
автор: Kolbajk