Question

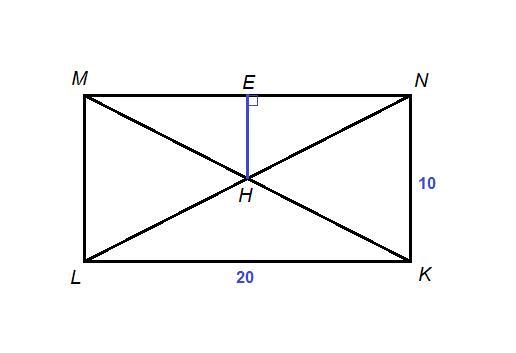
MNKL — прямоугольник со сторонами LK = 20 см, NK = 10 см, а н точка пересечения его диагоналей. Сколько точек пересечения имеет окружность с центром Н радиусом 6 см с прямой MN?​

Answer 1

Ответ:

Окружность с центром Н и прямая MN имеют две общие точки.

Объяснение:

Взаимное расположение прямой и окружности:

• если расстояние от центра окружности до прямой меньше радиуса, то прямая пересекает окружность (две общие точки);
• если расстояние от центра окружности до прямой равно радиусу, то прямая касается окружности (одна общая точка);
• если расстояние от центра окружности до прямой больше радиуса, то прямая пересекает и окружность не имеют общих точек.

• Противоположные стороны прямоугольника равны.

MN = LK = 20 см

ML = NK = 10 см

Проведем НЕ⊥MN, НЕ - расстояние от цетра окружности до прямой MN.

• Диагонали прямоугольника равны и точкой пересечения делятся пополам.

Н - середина МК,

НЕ║NK как перпендикуляры к одной прямой MN, тогда Е - середина MN по теореме Фалеса.

НЕ - средняя линия треугольника MNK.

НЕ = 0,5 NK = 0,5 · 10 = 5 см по свойству средней линии треугольника.

Радиус окружности R = 6 см, а расстояние до прямой MN равно 5 см.

Так как расстояние до прямой MN меньше радиуса, то прямая и окружность имеют 2 общие точки.