Предмет: Алгебра,
автор: Neyzka
Решить уравнение. ПОМОГИТЕ. С полным решением.
Приложения:
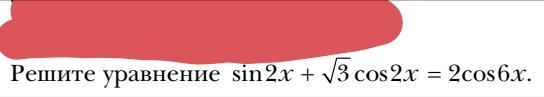
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: tsjjdnfcnncne
Предмет: Русский язык,
автор: юля2182
Предмет: Английский язык,
автор: FCPAHAN
Предмет: Физика,
автор: saginaev33