Question

Найди площадь боковой поверхности правильной четырёхугольной усечённой пирамиды, стороны оснований которой равны 22 и 6, а высота — 6.

Answer 1

Ответ:

S = (22^2 -6^2) 5/4 = 560

Объяснение:

Правильная пирамида

- в основании квадрат

- вершина падает в центр основания

Проекции боковых граней покрывают основание. Отношение площади проекции к исходной площади - косинус двугранного угла. Двугранные углы при основании равны. То есть основание относится к боковой поверхности как косинус двугранного угла при основании. Найдем этот угол.

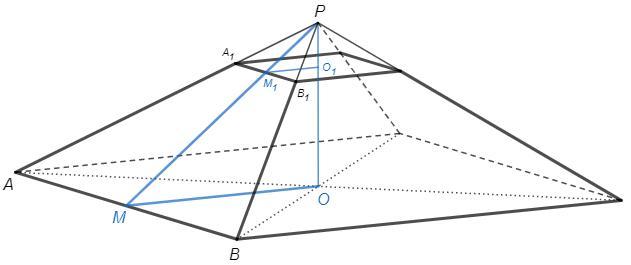
PM - апофема, ∠PMO - искомый угол.

Треугольники APB и A1PB1 подобны.

A1B1/AB =6/22 =PM1/PM =PO1/PO

OO1=6, OO1/PO=8/11 => PO=33/4

OM=AB/2=11, PO/OM=3/4 => cosM =OM/PM =4/5 (△PMO - египетский)

Sбок =Sосн/cosM

Площадь боковой поверхности усеченной пирамиды - разность боковых поверхностей исходной и отсекаемой пирамид.

S = 22^2 5/4 - 6^2 5/4 =560