Задание приложено...
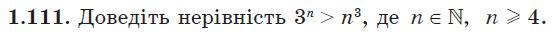
Ответы
Ответ:
Метод математической индукции:
Для того, чтобы доказать, что некоторое утверждение верно при натуральном необходимо выполнить следующие условия:
База индукции:
- 1) Доказать, что утверждение верно при
(или для любого другого конкретного натруального
, тогда утверждение будет доказано от
и до всех последюущих натуральных
если удастся доказать индуктивный переход).
Индуктивный переход:
- 2) Сделать гипотезу, что утверждение верно для
и на основании данной гипотезы доказать, что утверждение верно для
Если выполнены утверждения 1) и 2), то исходное утверждение доказано для всех натуральных методом математической индукции.
1.111
1) способ решения
Воспользуемся методом математической индукции:
База индукции:
- верно
Индуктивный переход:
- верно
Необходимо доказать:
Воспользуемся методом математической индукции:
при
База индукции:
- верно
Индуктивный переход:
- пусть верно
Необходимо доказать:
Воспользуемся методом математической индукции:
при
База индукции:
- верно
Индуктивный переход:
- верно
Необходимо доказать:
Так как - показательная функция, то
при
, а по условию минимальное
, то есть неравенство выпоняется при любых
.
Так как верно , то вся предыдущая серия неравенств также верна и методом математической индукции доказано, что
при
.