Предмет: Геометрия,
автор: Shadow9696
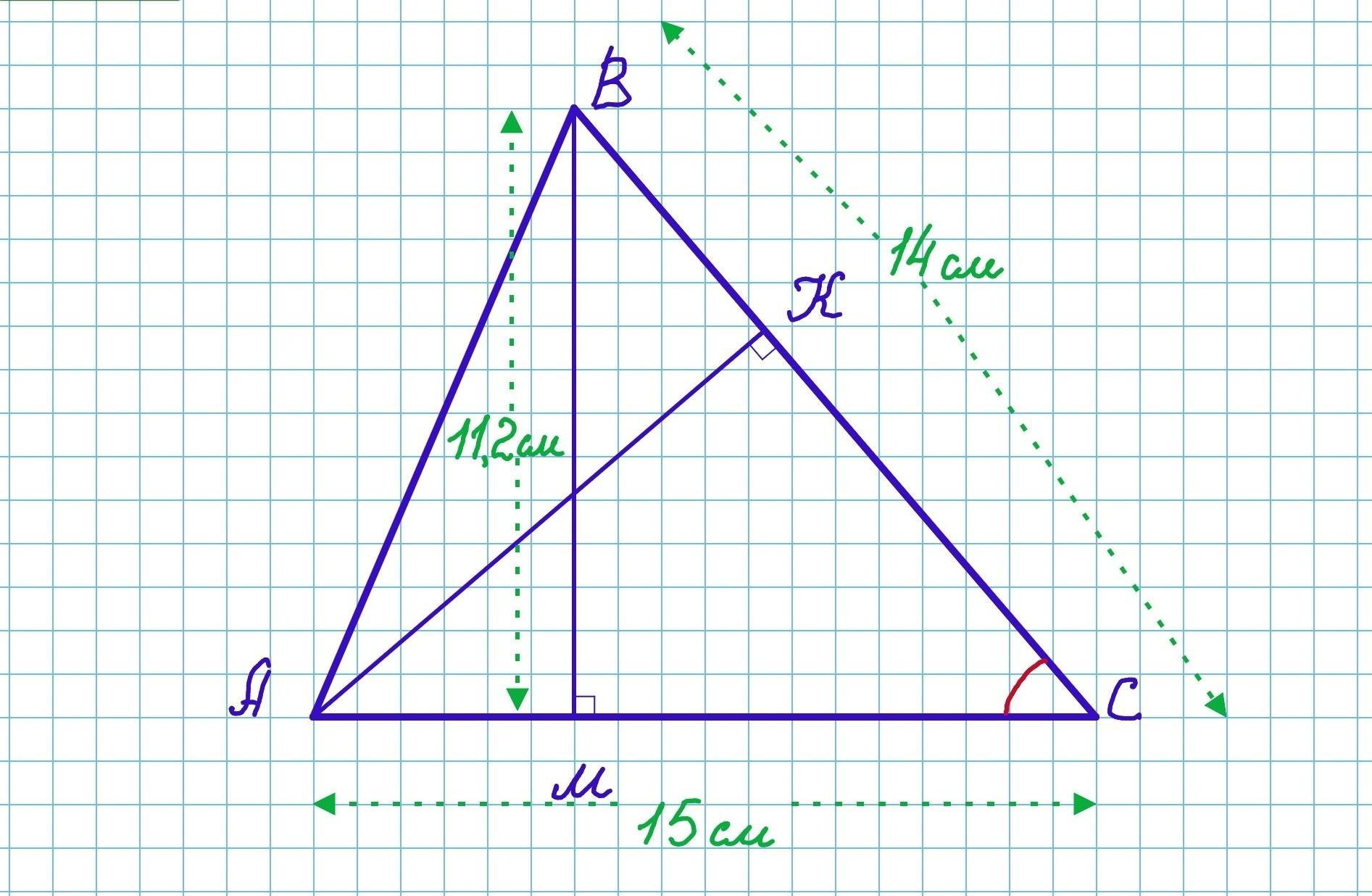
У гострокутному трикутнику АВС АС=15 см, ВС=14 см. АК і ВМ - висоти трикутника, ВМ =11,2 см. Знайдіть синус, косинус і тангенс кута С трикутника АВС.
Ответы
Автор ответа:
14
Ответ:
sin C = 0,8
cos C = 0,6
tg C = 4/3
Объяснение:
Дан остроугольный треугольник АВС. АК и ВМ - высоты треугольника. АК⟂ВС, ВМ⟂АС.
АС=15 см, ВС=14 см, ВМ=11,2см.
Найти sin C, cos C, tg C.
- Синус угла (sin С) - отношение противолежащего этому углу катета к гипотенузе.
- Косинус угла ( cos С) - отношение прилежащего катета к гипотенузе.
- Тангенс угла ( t g С) - отношение противолежащего катета к прилежащему.
1) Рассмотрим прямоугольный треугольник ВМС(∠М=90°, т.к. ВМ⟂АС)
Катет МС найдём по теореме Пифагора:
Тогда:
2) Косинус и тангенс угла С также можно найти другим способом.
Из основного тригонометрического тождества (sin²C+cos²C=1) находим cos C:
Теперь найдём тангенс угла С.
Известно, что:
Приложения:
andreykosenko2008:
а.
б.
Похожие вопросы
Предмет: Русский язык,
автор: вад34
Предмет: Другие предметы,
автор: софа20368
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: elenapronina03
Предмет: Астрономия,
автор: klimenkol21