Помогите пожалуйста
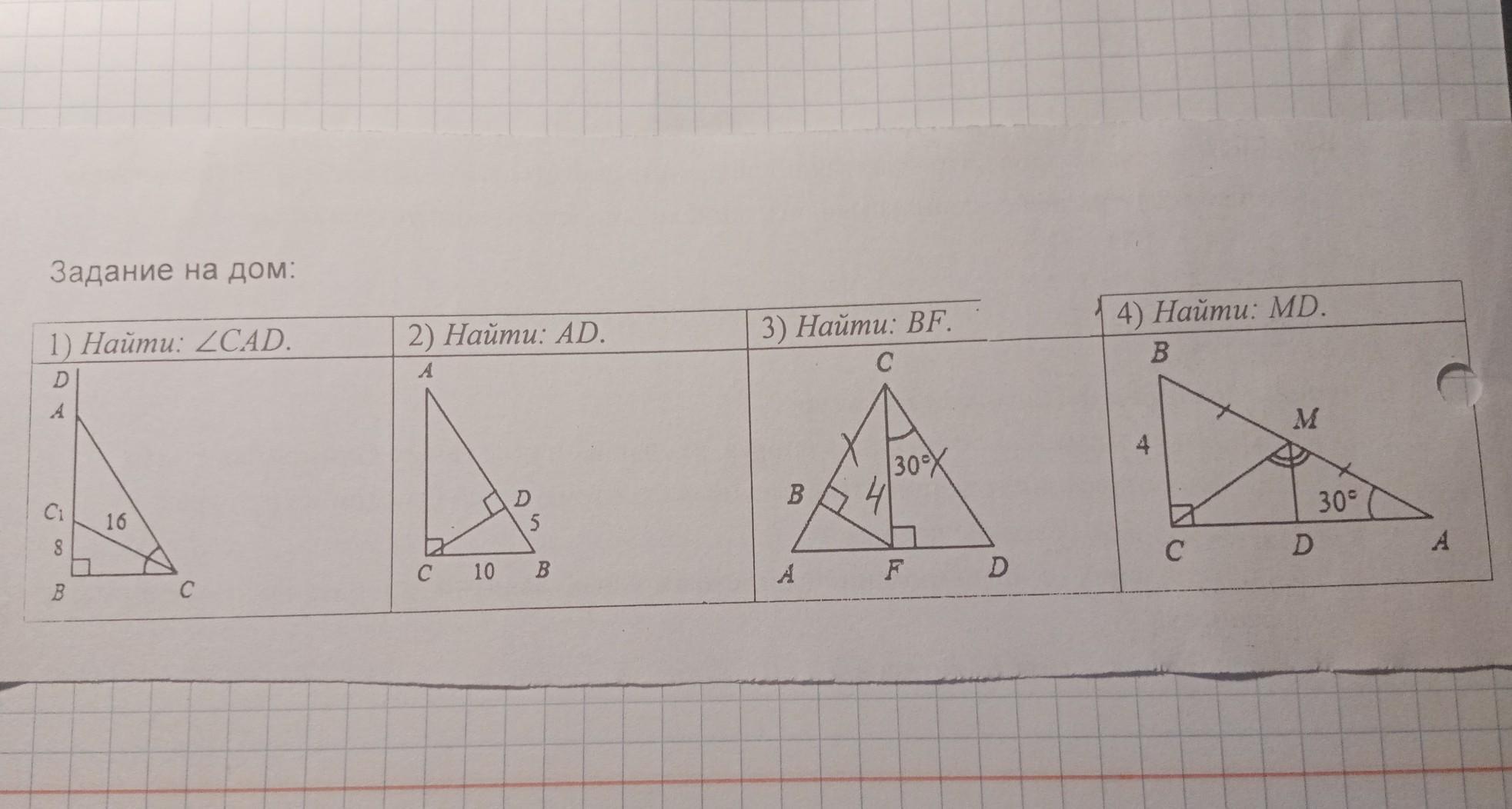
Ответы
Ответ:
1) ∠CAD = 150°. 2) AD = 15. 3) BF = 2. 4) 2.
Объяснение:
Катет против угла 30° равен половине гипотенузы.
Этот факт нам поможет во всех 4 задачах.
1) В прямоугольном треугольнике BCC1 катет BC1 = 8, а CC1 = 16.
Значит, угол ∠CC1B = 30°, угол ∠C1CA = 30°, потому что CC1 - биссектриса. Тогда угол ∠BCA = 60°, а угол ∠CAB = 30°
Угол ∠CAD = 180° - 30° = 150°.
2) В прямоугольном треугольнике BCD катет BD = 5, а BC = 10.
Значит, угол ∠BCD = 30°, угол DCA = 60°, а угол DAC = 30°.
По теореме Пифагора
CD^2 = BC^2 - BD^2 = 10^2 - 5^2 = 100 - 25 = 75
CD = √75 = 5√3
В треугольнике ACD опять гипотенуза AC = 2*CD = 2*5√3 = 10√3
AD^2 = AC^2 - CD^2 = (10√3)^2 - (5√3)^2 = 300 - 75 = 225
AD = 15
3) Треугольник ACD - равнобедренный, значит, CF - высота и медиана.
Угол ∠BCF = ∠FCD = 30°.
В треугольнике BCF гипотенуза CF = 4, значит катет
BF = 4/2 = 2.
4) В прямоугольном треугольнике ABC угол ∠CAB = 30°, ∠ABC = 60°.
Треугольник CMA - равнобедренный с углами 30°, 30° и 120°.
Угол ∠CMD = ∠DMA = 120°/2 = 60°
Угол ∠CMB = ∠CBM = 60°
Треугольник CMB - равнобедренный с углом 60°, то есть равносторонний.
CB = BM = CM = AM = 4
В прямоугольном треугольнике DMA углы 30°, 60° и 90°.
Катет против угла 30° MD = AM/2 = 4/2 = 2.