Предмет: Геометрия,
автор: 01YES
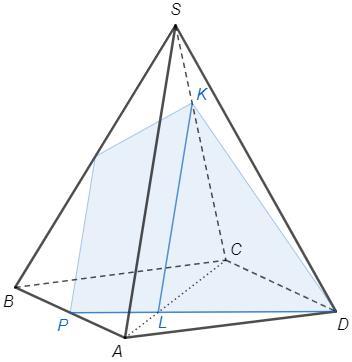
В правильной четырёхугольной пирамиде SABCD точка K на ребре SC выбрана так, что SK : SC = 1 : 3. Плоскость, проходящая через точки K и D параллельно прямой АS, пересекает прямую АB в точке Р. Найдите отношение АР : РB.
Ответы
Автор ответа:
1
Пусть плоскости ASC и KDP пересекаются по прямой KL.
Прямая AS параллельна плоскости KDP, следовательно не имеет общих точек с прямой KL.
Прямые AS и KL лежат в плоскости ASC и не имеют общих точек, следовательно параллельны, AS||KL.
AL/LC =SK/KC =1/2 (по т о пропроциональных отрезках)
△ALP~△CLD => AP/CD =AL/LC =1/2 => AP/PB=1/1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: krasnova4
Предмет: Окружающий мир,
автор: natalia178
Предмет: Черчение,
автор: ОгУрЕчНиК
Предмет: История,
автор: alinka0336
Предмет: Литература,
автор: corobka337