Предмет: Математика,
автор: Санякоторыйсмог
В квадрате со сторой 3 проведены две дуги с радиусом 3 (см рисунок). Найдите площать закрашенной фигуры.
Приложения:
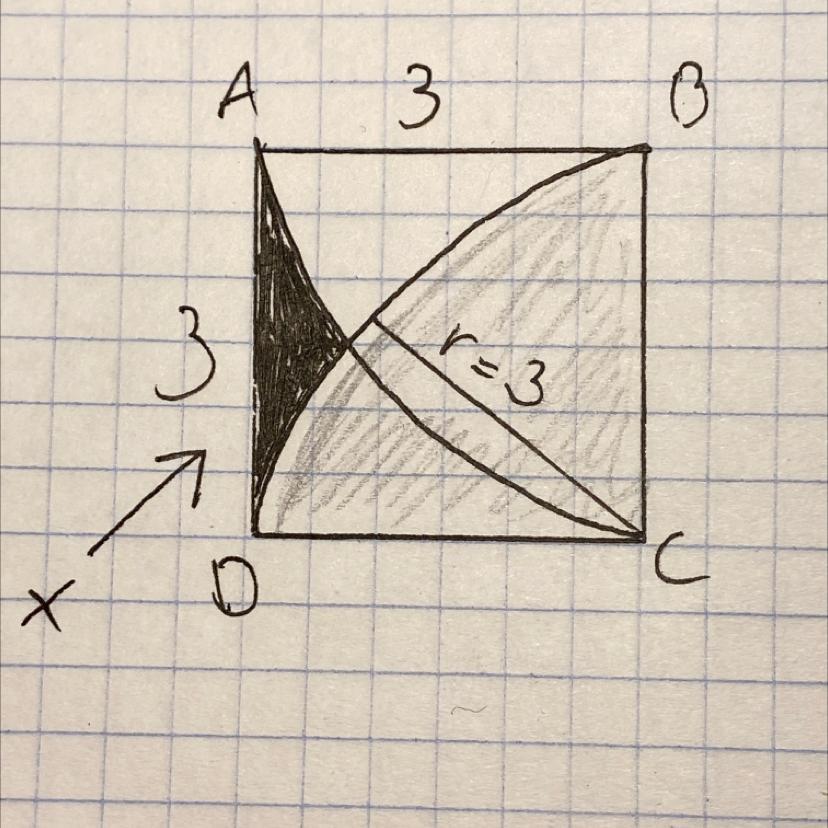
Санякоторыйсмог:
Помогите пожалуйста мне срочно надо!!!
Ответы
Автор ответа:
2
Ответ:
a^2*(1-sqrt(3)/4-pi/6)
Пошаговое объяснение:
Пусть М - точка пересечения дуг АС и DB
Очевидно отрезки СМ и ВМ равны.Но ВМ=ВС
Значит треугольник ВМС - равносторонний со стороной а.
Его площадь a^2*sqrt(3)/4=S1
Площадь сектора ВМС=pi*a^2/6 (центральный угол 60 гр)
Площадь лунки, образованной дугой МС и хордой МС равна
pi*a^2/6-S1
Площадь фигуры ВМС, образованной дугами МС и МВ и стороной ВС равна сумме площади сектора ВМС и точно такой же лунки
Площадь фигуры ВМС=pi*a^2/6-S1+pi*a^2/6=pi*a^2/3-a^2*sqrt(3)/4=S2
Площадь сектора АВС равна pi*a^2/4=S3
Искомая площадь a^2-2*S3+S2= a^2-pi*a^2/2+pi*a^2/3-a^2*sqrt(3)/4=
a^2*(1-sqrt(3)/4-pi/6)
Спасибо! А sqrt это что
sqrt -корень квадратный.
Похожие вопросы
Предмет: Українська мова,
автор: Даня01122006
Предмет: Окружающий мир,
автор: kitkha
Предмет: Русский язык,
автор: Джора03
Предмет: Математика,
автор: yanav2901
Предмет: Математика,
автор: ЛаймGM25