Предмет: Математика,
автор: Unicorn1402
решить уравнение (12 задание егэ)
пожалуйста:(
Приложения:
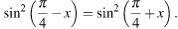
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Перенесём из правой части в левую:
Применим формулу разности квадратов:
Равенство выполняется, если
1)
или
2)
Решим 1-е уравнение, применив формулу разности синусов:
Решим 2-е уравнение с помощью формулы суммы синусов:
Решения можно объединить в 1-у серию: (здесь и ранее k - целое число)
Похожие вопросы
Предмет: Русский язык,
автор: Дарьяcom1
Предмет: Русский язык,
автор: maksimsenchenko
Предмет: Английский язык,
автор: патрисия2
Предмет: История,
автор: MilaPrincessa0416
Предмет: Английский язык,
автор: dimazhdanov2002