Question

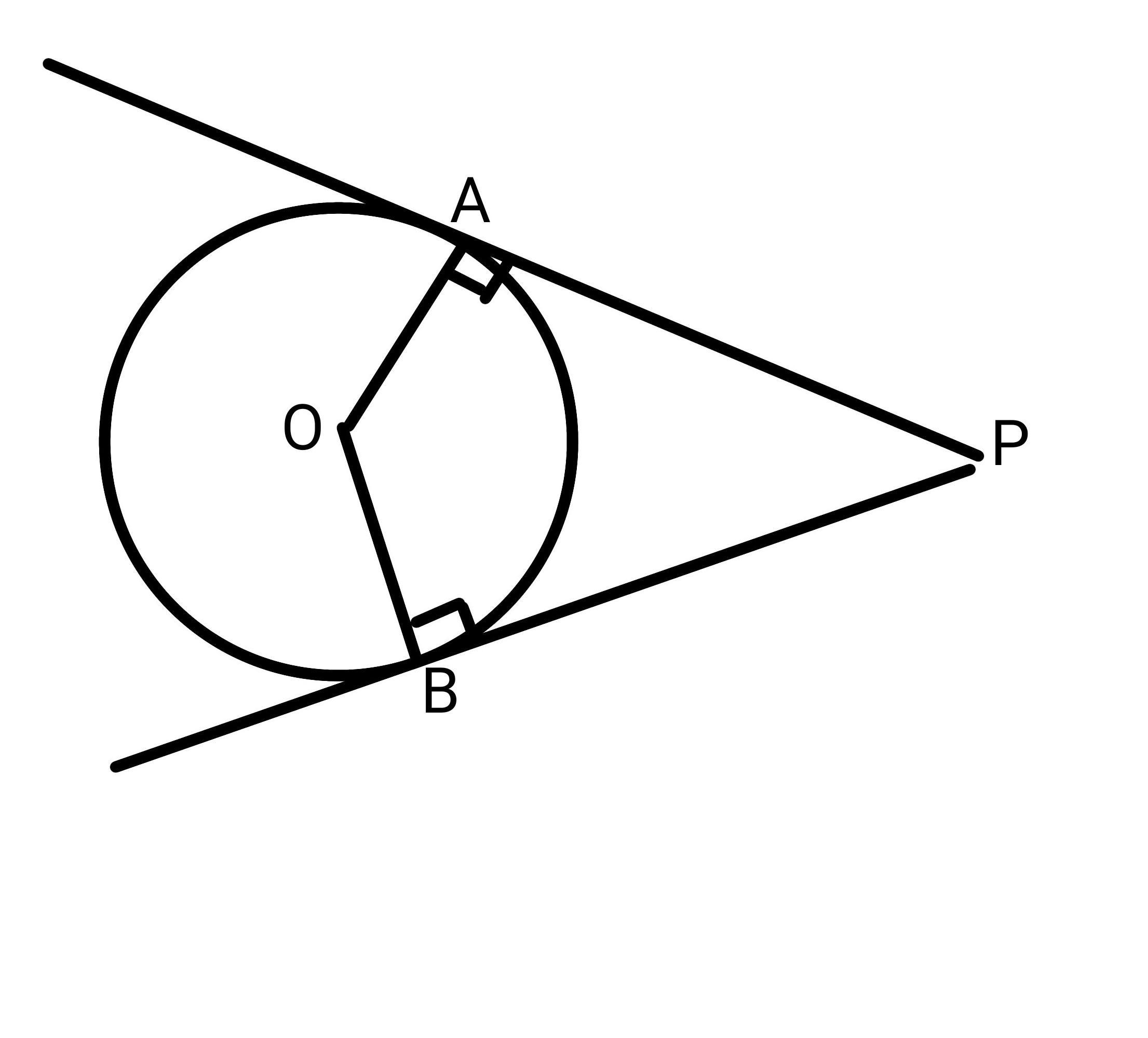
Найдите угол между УГОЛ между касательными, касательными, проведенными ИЗ ТОЧКИ, внешней по отношению к окружности, если точки касания делят Окружность на две дуги, относящиеся как: 3:15​

Answer 1

Ответ:

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны, поэтому углы ∠PBO=∠PAO=90°

Найдем меньший угол AOB=3x, а больший 15x.

Общий угол окружности 360°.

$3x + 15x = {360}^{ \circ} \\ 18x = {360}^{ \circ} \\ x = {20}^{ \circ}$

Нам нужен меньший 3x.

3x=3×20°=60°.

PAOB – четырехугольник, сумма внутренних углов четырехугольника 360°.

∠PAO+∠AOB+∠OBP+∠APB=360°

90°+60°+90°+∠APB=360°

240°+∠APB=360°

∠APB=360°-240°

∠APB=120°

∠APB – это и есть нужный нам угол между касательными.