Предмет: Алгебра,
автор: lizapogorelaia66
даю 25 баллов!!! СРОЧНО помогите пожалуйста
Приложения:
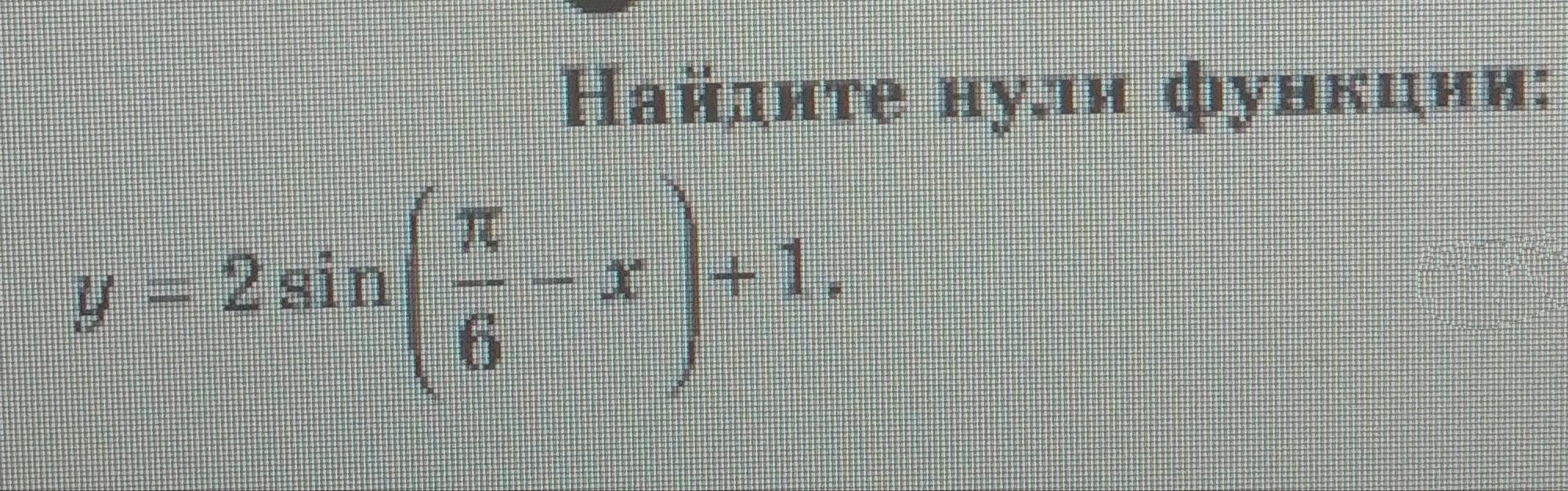
Ответы
Автор ответа:
0
Ответ:
Чтобы найти нули функции, приравняем эту функцию нулю .
lizapogorelaia66:
можешь помочь. я выложила там ещё номер. даю 30 баллов
помоги пожалуйста
Похожие вопросы
Предмет: Французский язык,
автор: ecnz1
Предмет: Қазақ тiлi,
автор: Хакер365
Предмет: Русский язык,
автор: Губка00Боб
Предмет: Физика,
автор: Pqpqgg