Предмет: Геометрия,
автор: twitchlox86
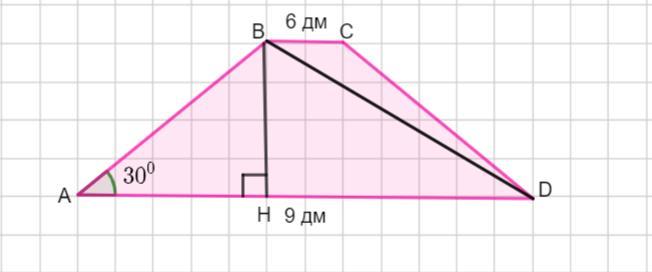
В равнобедренной трапеции основания равны 9 дм и 6 дм, а острый угол равен 30°. Найди диагональ трапеции.
Ответы
Автор ответа:
1
Ответ:
Диагональ трапеции равна √57 дм.
Объяснение:
Пусть дана равнобедренная трапеция АВСD.
АD = 9 дм , ВС= 6 дм.
Проведем высоту ВН, если трапеция равнобедренная, то
АН = ( 9-6):2=3:2 = 1,5 дм.
Рассмотрим Δ АНВ - прямоугольный, ∠А=30° по условию.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
дм
Расcмотрим Δ BHD - прямоугольный.
HD=АD - АН;
HD=9-1,5= 7,5 дм.
Найдем диагональ трапеции BD, как гипотенузу прямоугольного треугольника по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Тогда диагональ трапеции равна √57 дм.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: olega51ru
Предмет: Қазақ тiлi,
автор: DOBLEKILL
Предмет: Русский язык,
автор: anonimus69
Предмет: Английский язык,
автор: shestopal723
Предмет: Литература,
автор: sasasatynov21