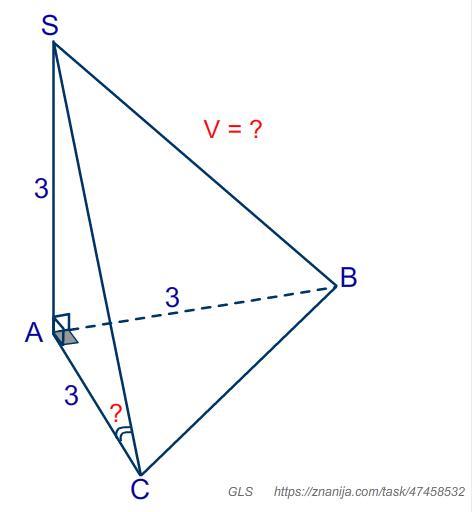
В треугольной пирамиде SABC основание-треугольник ABC, угол А=90. Ребро SA перпендикулярно плоскости основания. SA=AB=AC=3. Найдите объем и угол наклона ребра SC к плоскости основания
ПОМОГИТЕ ПОЖАЛУЙСТА!!!!!!!!
Ответы
Ответ:
Угол наклона ребра SC к плоскости основания равен 45°, объем пирамиды 4,5 куб. ед.
Объяснение:
В треугольной пирамиде SABC основание - треугольник ABC, ∠А=90°. Ребро SA перпендикулярно плоскости основания. SA = AB = AC = 3. Найти объем пирамиды и угол наклона ребра SC к плоскости основания.
Дано:
SABC - пирамида;
ABC - основание, ∠A = 90°;
SA ⊥ ABC;
SA = AB = AC = 3.
Найти: ∠SCA; V
Решение.
- Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
1) Ребро пирамиды SA ⊥ плоскости основания по условию, тогда
ребро SA перпендикулярно стороне основания AC
SA ⊥ AC.
2) Угол наклона ребра SC к плоскости основания - это угол между наклонной и ее проекцией - это ∠SCA:
SC - наклонная, AC - ее проекция - отрезок, соединяющий основание наклонной и основание перпендикуляра, проведенных из одной точки S.
3) ΔSAC прямоугольный и равнобедренный:
∠SAC = 90°, по условию SA = AC = 3.
В равнобедренном треугольнике углы при основании равны.
Тогда ∠SCA = (180° - 90° ) : 2 = 45°.
- Площадь прямоугольного треугольника равна половине произведения его катетов.
Объем пирамиды равен одной третьей произведения основания на высоту: V = (1/3) · Sосн · H.
4) Найдем площадь основания пирамиды.
(кв. ед).
5) Найдем объем пирамиды.
(куб. ед).
Угол наклона ребра SC к плоскости основания равен 45°, объем пирамиды 4,5 куб. ед.