Question

Дан шар диаметром 30 см. Стороны квадрата ABCD касаются поверхности шара. Расстояние от центра шара до плоскости квадрата равно 9 см. Найдите площадь квадрата.

Answer 1

Ответ:

576 см^2

Объяснение:

Дан шар с диаметром D = 30 см, R = D/2 = 30/2 = 15 см

Его пересекает плоскость квадрата ABCD, который касается поверхности шара. Расстояние от центра шара O до плоскости квадрата равно H = 9 см.

Найти площадь квадрата.

Решение:

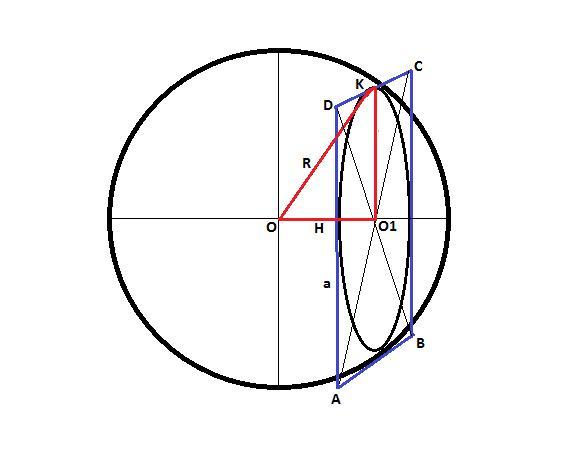
Смотрите рисунок.

Квадрат я нарисовал синим цветом, а отрезки красным.

Стороны квадрата касаются поверхности шара - значит, сечение шара с центром O1 и радиусом O1K является вписанным в квадрат.

Треугольник OO1K - прямоугольный. Из теоремы Пифагора:

OK^2 = OO1^2 + O1K^2

O1K^2 = OK^2 - OO1^2 = 15^2 - 9^2 = 225 - 81 = 144

O1K = √144 = 12 см

Но радиус окружности, вписанной в квадрат, равен половине стороны квадрата.

AB = BC = CD = DA = a = 2*O1K = 2*12 = 24 см

Площадь квадрата:

S = a^2 = 24^2 = 576 см^2