Предмет: Алгебра,
автор: Lqdqiaq
Помогите пожалуйста срочно докажите тождество
Приложения:
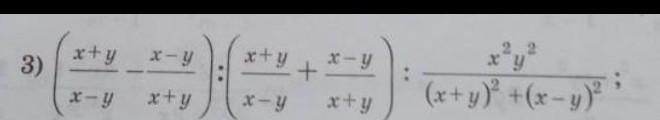
Ответы
Автор ответа:
0
Объяснение:
3.
Похожие вопросы
Предмет: Другие предметы,
автор: саря1
Предмет: Русский язык,
автор: elizavetaklimenko68
Предмет: Английский язык,
автор: vkkaskov
Предмет: История,
автор: Sayrma2228
Предмет: Другие предметы,
автор: uzunovalissa