Question

1) Объем шара равен 24Пи см^3. Найдите площадь
сферы, ограничивающей этот шар.
2) В шаре радиуса 20 см проведено сечение,
площадь которого равна 100Пи см^3. Найдите объем
меньшего шарового сегмента, отсекаемого плоскостью сечения.
3) Найдите объем шарового сектора, если радиус
шара равен 5 см, а высота соответствующего
сегмента составляет пятую часть диаметра
шара.

Answer 1

Ответ:

1) 12π*∛12 см^2; 2) 2000π*(2 - √3)/3 см^3; 3) 112/3*π см^3

Объяснение:

1) Объём шара можно вычислить по формуле:

V = 4/3*π*R^3 = 24π

R^3 = 24*3/4 = 6*3 = 18

R = ∛18 см

Площадь сферы можно вычислить по формуле:

S = 4π*R^2 = 4π*(∛18)^2 = 4π*∛(4*81) = 4*3π*∛(4*3) = 12π*∛12 см^2

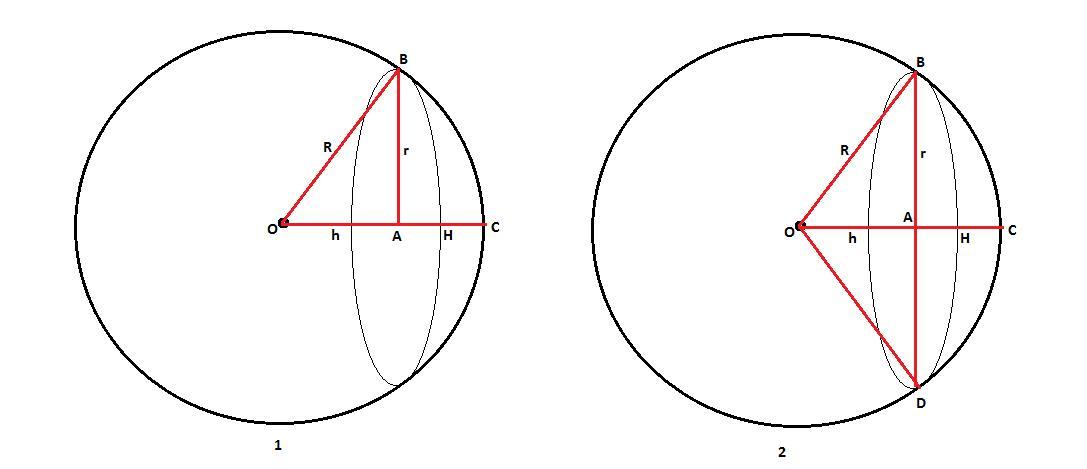
2) R = 20 см. Площадь центрального сечения:

S(ц.с.) = π*R^2 = π*20^2 = 400π см^2

Смотрите рисунок 1.

Площадь проведённого сечения:

S(сеч) = 100π = π*r^2 см^2.

r^2 = 100

r = 10 см

По теореме Пифагора для треугольника OAB:

OA^2 = OB^2 - AB^2

h^2 = R^2 - r^2 = 400 - 100 = 300 см^2

h = √300 = 10√3 см

Высота шарового сегмента:

AC = H = R - h = 20 - 10√3 = 10*(2 - √3) см

Объём шарового сегмента с радиусом r см и высотой H см:

V = 2/3*π*r^2*H = 2/3*π*100*10(2 - √3) = 2000π*(2 - √3)/3 см^3

3) Радиус шара R = 5 см.

Смотрите рисунок 2.

Высота шарового сегмента H = 2R/5 = 2*5/5 = 2 см

Высота конуса OBD: h = R - H = 5 - 2 = 3 см.

Шаровой сектор состоит из конуса OBD и сегмента BCD:

Радиус сечения найдём из теоремы Пифагора:

r^2 = R^2 - h^2 = 5^2 - 3^2 = 25 - 9 = 16

r = 4 см

Объём шарового сегмента с радиусом r см и высотой H см:

V(сег) = 2/3*π*r^2*H = 2/3*π*16*2 = 64/3*π см^3

Объём конуса:

V(кон) = 1/3*π*r^2*h = 1/3*π*4^2*3 = 16π = 48/3*π см^3

Объём шарового вектора:

V(сек) = 64/3*π + 48/3*π = 112/3*π см^3