Question

Вопрос 4
Острые углы прямоугольного треугольника равны 20º и 70º. Найдите угол между высотой и медианой проведенными из вершины прямого угла. Ответ дайте в градусах.

Answer 1

Ответ:

50°

Объяснение:

Острые углы прямоугольного треугольника равны 20º и 70º. Найдите угол между высотой и медианой проведенными из вершины прямого угла. Ответ дайте в градусах.

решение на фото

Answer 2

Ответ:

Угол между высотой и медианой = 50°

Объяснение:

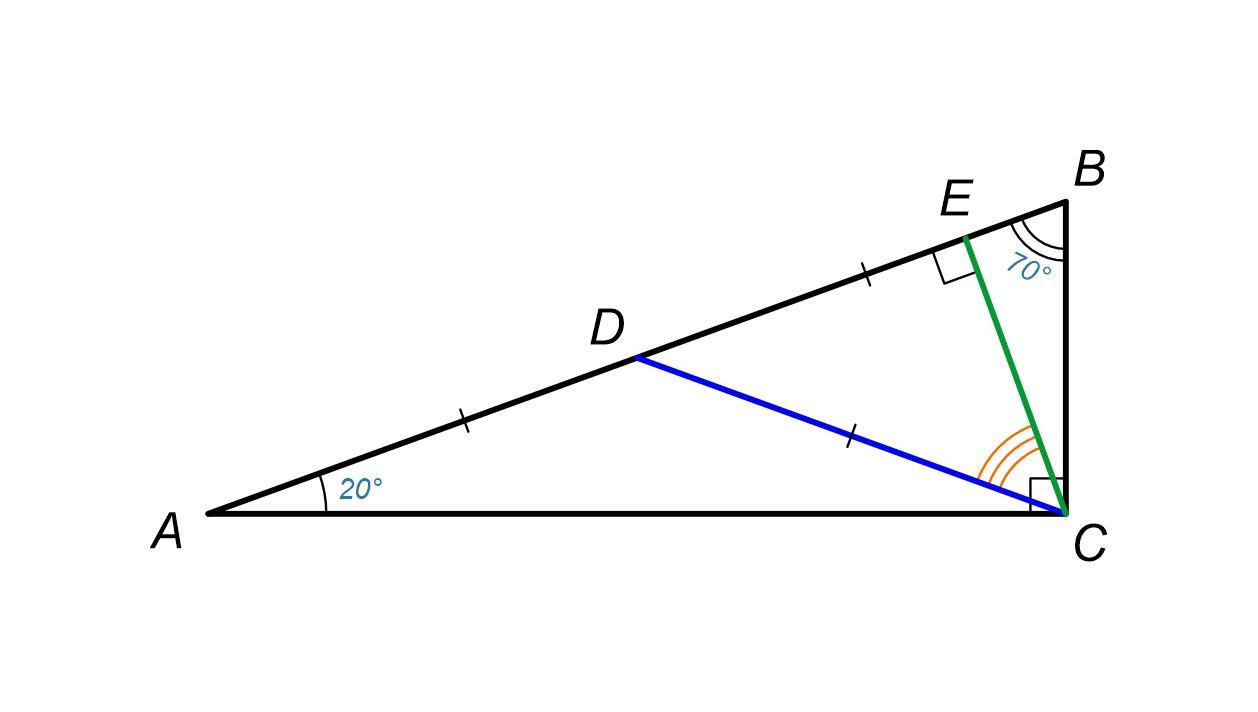
Рассмотрим ΔBEC - это прямоугольный треугольник, у которого ∠EBC = 70°; ∠BEC = 90°; ∠BCE - ?

Известно что сумма углов любого треугольника = 180° ⇒

180° = ∠EBC + ∠BEC + ∠BCE

180° = 70° + 90° + ∠BCE

∠BCE = 180° - 160°

∠BCE = 20°

Есть такая Теорема: В прямоугольном треугольнике медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы ⇒ AD = DB = DC

Рассмотрим ΔDBC - это равнобедренный треугольник, у которого DB = DC, ⇒ углы при основании BC равны, тоесть ∠DBC = ∠DCB = 70°

Угол между высотой и медианой это ∠DCE = ∠DCB - ∠BCE = 70° - 20° = 50°