Предмет: Алгебра,
автор: skwindi12
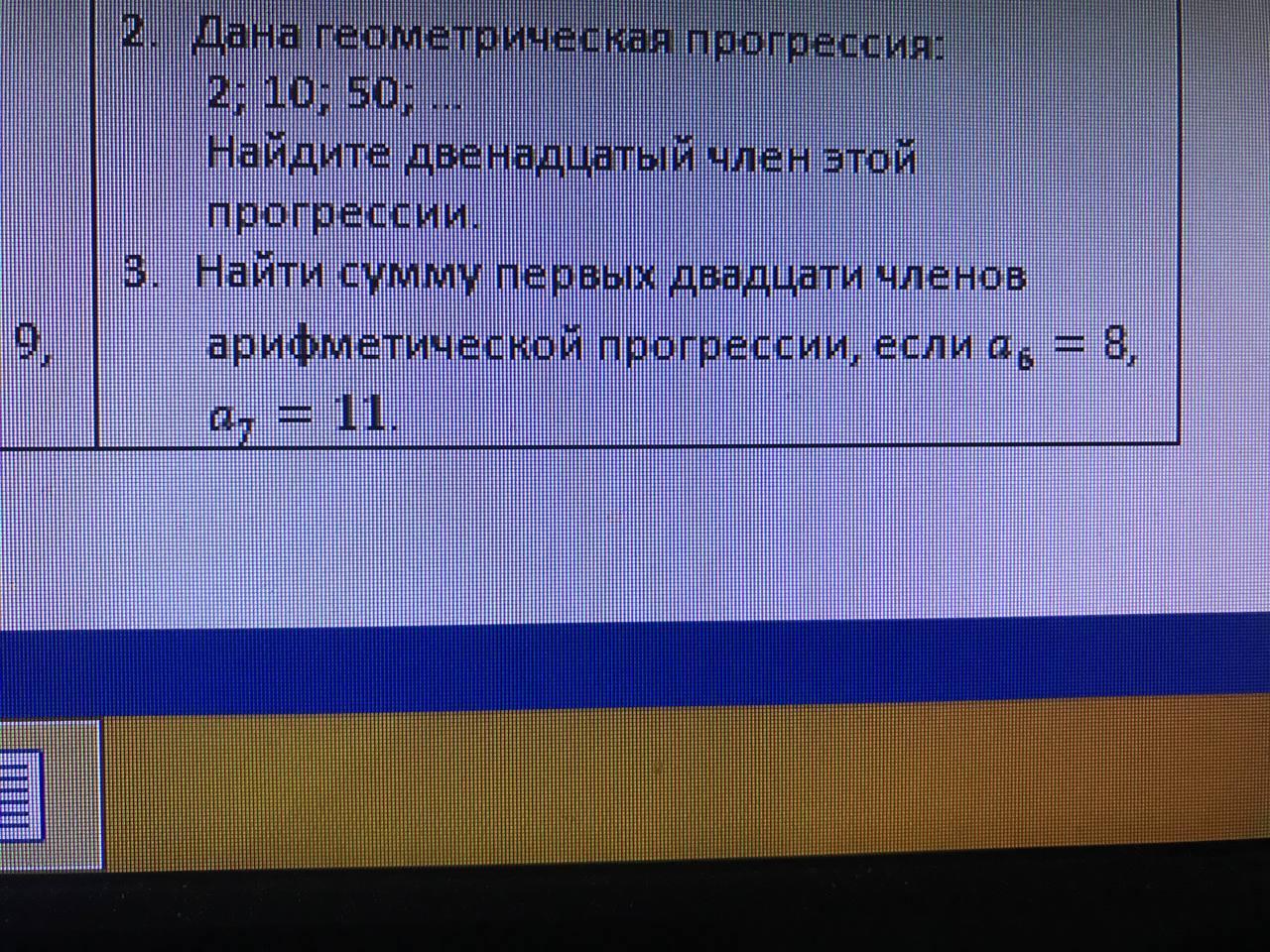
Решите пожалуйста 3,4,5 спасибо
Приложения:

Ответы
Автор ответа:
8
Ответ:
Объяснение:
составим уравнение согласно характеристическому свойству арифметической прогрессии :
Похожие вопросы
Предмет: Русский язык,
автор: ДанаТомирис
Предмет: Русский язык,
автор: 89097748841
Предмет: Қазақ тiлi,
автор: dayald09
Предмет: Русский язык,
автор: polinashka5
Предмет: Математика,
автор: ponomarenko18nastenk