Question

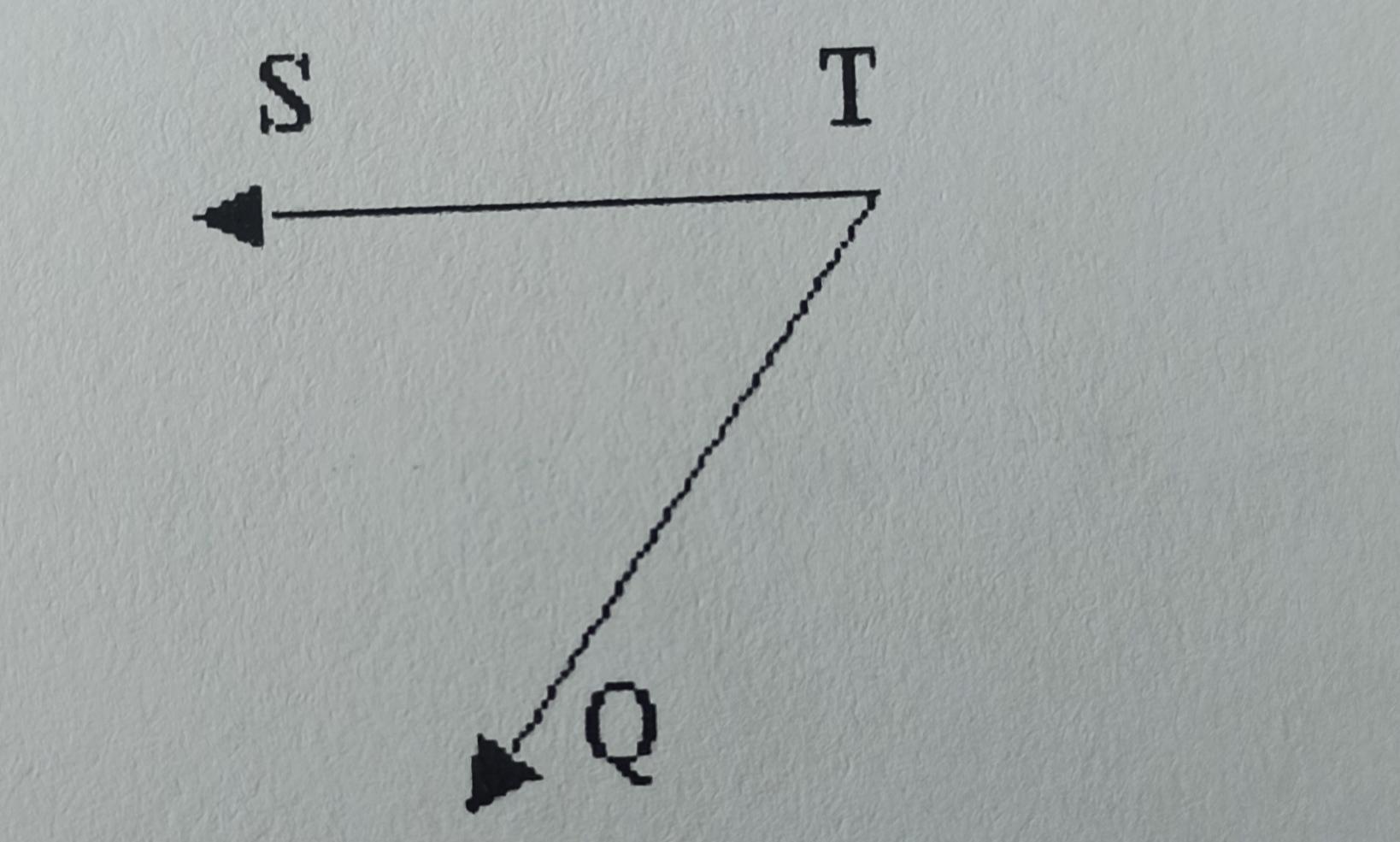
Постройте вектор равный разности векторов TQ-TS. запишите результат в виде равенства

Answer 1

Ответ:

Разность заданных векторов:    $\displaystyle \overrightarrow{TQ} - \overrightarrow{TS} = \overrightarrow{SQ}$

Объяснение:

Постройте вектор, равный разности векторов TQ - TS. Записать результат в виде равенства.

• Разностью векторов $\displaystyle \vec{a}$ и $\displaystyle \vec{b}$ называется такой вектор $\displaystyle \vec{c}$, который в сумме с вектором $\displaystyle \vec{b}$ даст вектор $\displaystyle \vec{a}.$
  $\displaystyle \vec{a} - \vec{b}= \vec{c},$ если $\displaystyle \vec{c} + \vec{b}= \vec{a}$.
• Два вектора называются противоположными, если они равны по модулю и противоположно направлены.

Чтобы найти разность векторов  $\displaystyle \overrightarrow{TQ} - \overrightarrow{TS}$,  нужно найти сумму вектора $\displaystyle \overrightarrow{TQ}$  и вектора, противоположного вектору $\displaystyle \overrightarrow{TS}$:

$\displaystyle \overrightarrow{TQ} - \overrightarrow{TS} = \overrightarrow{TQ} + (-\overrightarrow{TS})=\overrightarrow{TQ} + \overrightarrow{ST}.$

Свойство сложения векторов коммутативно:
$\displaystyle \overrightarrow{TQ} + \overrightarrow{ST} = \overrightarrow{ST} + \overrightarrow{TQ}.$

• Чтобы сложить два вектора по правилу треугольника, нужно с помощью параллельного переноса совместить начало второго вектора с концом первого вектора.
  Вектор, соединяющий начало первого и конец второго векторов, является их суммой.

Найдем сумму векторов  $\displaystyle \overrightarrow{TQ} + \overrightarrow{ST}$ по правилу треугольника.

Конец вектора $\displaystyle \overrightarrow{ST}$ совпадает с началом вектора $\displaystyle \overrightarrow{TQ}.$

Тогда вектор  $\displaystyle \overrightarrow{SQ}$ , соединяющий начало вектора $\displaystyle \overrightarrow{ST}$ и конец вектора  $\displaystyle \overrightarrow{TQ}$ является суммой этих векторов.

Таким образом, разность заданных векторов

$\displaystyle \overrightarrow{TQ} - \overrightarrow{TS} = \overrightarrow{TQ} + (-\overrightarrow{TS})=\\\\\\= \overrightarrow{TQ} + \overrightarrow{ST} =\overrightarrow{ST} + \overrightarrow{TQ} = \overrightarrow{SQ}$