Question

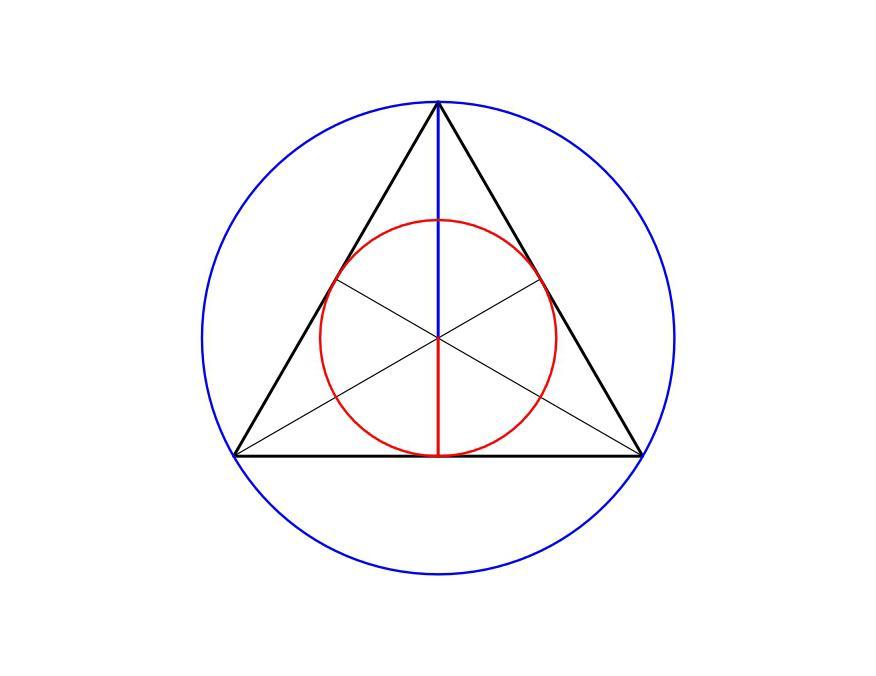
Обчислити сторону правильного трикутника і радіус вписаного в нього кола, якщо радіус кола, описаного навколо даного трикутника, дорівнює 4 см.​

Answer 1

Ответ:

Сторона правильного треугольника = $\frac{12}{\sqrt{3}}$ см

Радиус вписанного в него круга = 2 см

Пошаговое объяснение:

В правильном треугольнике точка пересечения диагоналей делит эти диагонали по правилу 2 : 1

R - Радиус описанной окружности = 4 см

r - Радиус вписаной окружности = x см

Составим пропорцию:

$\frac{4}{x} = \frac{2}{1} \\\\x = \frac{4*1}{2} = 2 cm$

В нашем случае высота равностороннего треугольника равна:

h = r + R = 2 + 4 = 6 cm

Так же высота равностороннего треугольника вычисляется по формуле:

$h = \frac{\sqrt{3}}{2}a$, где a - сторона равностороннего треугольника.

⇒ $a = h:\frac{\sqrt{3}}{2} = \frac{2h}{\sqrt{3}} = \frac{2*6}{\sqrt{3}} = \frac{12}{\sqrt{3}}$