Question

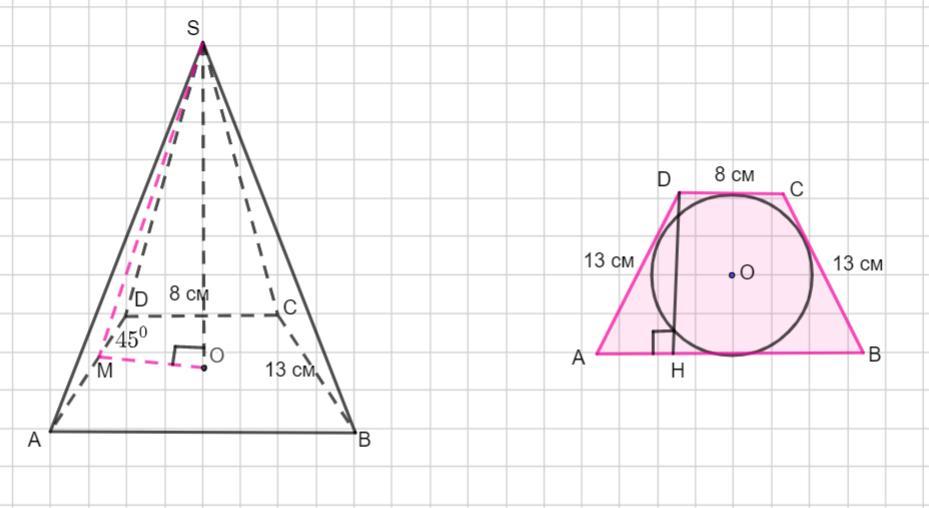
В основі піраміди лежить рівнобічна трапеція з бічною стороною 13 см і меншою
основою 8 см. Знайдіть об'єм піраміди, якщо її бічні грані нахилені до площини
основи під кутом 45

Answer 1

Ответ:

Объем пирамиды равен 312 см³.

Объяснение:

Пусть дана пирамида $SABCD.$

Основание пирамиды равнобедренная трапеция $ABCD.$

AD= BC =13 см , DC= 8 см.

Все боковые грани наклонены к плоскости основания под углом 45°. Если все боковые грани наклонены к плоскости основания под одним углом, то вершина пирамиды проектируется в центр вписанной окружности. Значит, ОМ - радиус, вписанной в трапецию окружности.

Найдем радиус окружности, вписанной в равнобедренную трапецию. Диаметр этой окружности равен высоте трапеции.

Если окружность вписана в четыреугольник, то суммы противолежащих сторон равны.

AB+CD= AD+BC =13+13 =26 cм

AB= 26 - 8 =18 см.

Если трапеция равнобедренная, то

АН = (18-8):2=10 : 2 = 5 см.

Рассмотрим Δ AHD - прямоугольный.

Найдем катет HD  по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AD^{2} =AH^{2} +HD^{2} ; \\HD^{2}=AD^{2} =AH^{2};\\HD=\sqrt{AD^{2} =AH^{2}} ;\\HD=\sqrt{13^{2}-5^{2} } =\sqrt{169-25} =\sqrt{144} =12$

Если высота трапеции равна 12 см, то радиус вписанной окружности равен 12 : 2 = 6 см.

Тогда ОМ= 6 см.

Рассмотрим ΔSOM - прямоугольный, если ∠SM0=45°, то ∠МSO=90°-45°=45° и ΔSOM - прямоугольный и равнобедренный.

SO =ОМ =6 см.

Тогда высота пирамиды равна 6 см.

Найдем площадь основания пирамиды, то есть площадь трапеции.

Площадь трапеции равна произведению полусуммы оснований на высоту.

$S= \dfrac{AB+DC}{2} \cdot DH;\\\\S= \dfrac{18+8}{2} \cdot 12=\dfrac{26}{2}\cdot12=13\cdot12=156 .$

Площадь трапеции равна 156 см².

Найдем объем пирамиды по формуле:

$V= \dfrac{1}{3} \cdot S\cdot H,$

где S- площадь основания пирамиды,  H- высота пирамиды.

$V= \dfrac{1}{3} \cdot 156\cdot6=156\cdot2=312$  

Объем пирамиды равен 312 см³.