Предмет: Геометрия,
автор: tarakanshark
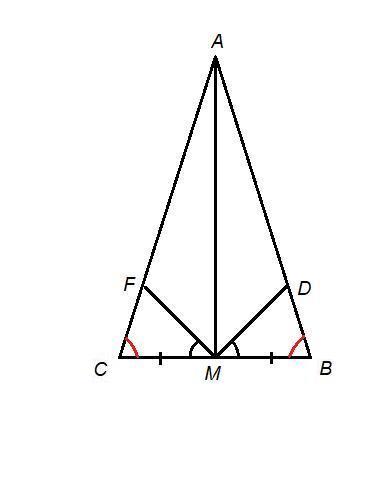
У трикутнику ABC ∠C = ∠B, AM – медіана. На сторонах АС і AB відповідно позначено точки F i D так, що ∠FMC = ∠DMB. Які відрізки однакової довжини при цьому утворилися? Відповідь обґрунтуйте. малюнок обов,язково
Ответы
Автор ответа:
6
Ответ:
Получились равные отрезки:
ВМ = МС
АВ = АС
FС = DВ
FM = DM
AF = AD
Объяснение:
ВМ = МС, так как АМ медиана.
В треугольнике АВС ∠В = ∠С, значит треугольник равнобедренный, АВ = АС.
ΔFMC = ΔDMB по стороне и двум прилежащим к ней углам:
- ВМ = МС, так как АМ медиана;
- ∠В = ∠С по условию;
- ∠FMC = ∠DMB по условию.
Значит, FС = DВ и FM = DM.
AF = AС - FС,
AD = AB - DB.
Так как АВ = АС и DB = FC, то AF = AD.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kuzinka96
Предмет: Русский язык,
автор: 777emylee777
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: kostz77
Предмет: Алгебра,
автор: Товарищ228