Question

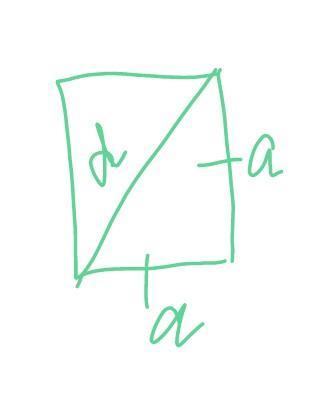
довжина діагоналі квадрата дорівнює
$6 \sqrt{3}$
сантимерів. Обчисліть його площу​

Answer 1

Ответ:

54 см^2

Объяснение:

У квадрата стороны равны.

По теореме Пифагора есть уравнение:

${a}^{2} + {a}^{2} = (6 \sqrt{3} ) {}^{2} \\ 2a {}^{2} = 6 {}^{2} { (\sqrt{3}) }^{2} \\ 2a {}^{2} = 36 \times 3 \\ 2a {}^{2} = 108 \\ {a}^{2} = 108 \div 2 \\ {a}^{2} = 54 \\ a = \sqrt{54}$

Поскольку длина стороны не может быть отрицательной, то -√54 не удовлетворяет условию.

Площадь квадрата равна S = a^2, отсюда

$( \sqrt{54} ) {}^{2} = 54.$