Предмет: Алгебра,
автор: Аноним
Найдите значение выражения: 5cos(a - b), если cosa*cosb = 1/2; a + b = п/3.
4)4sin(a-b),если sina cosb=1/4;a+b=-π/6
Приложения:
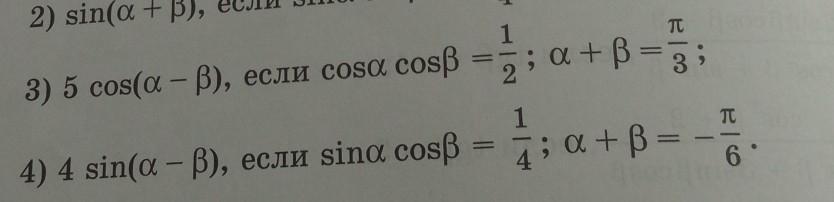
Ответы
Автор ответа:
2
Universalka:
Перезагрузите и проверьте я немного исправила .
Похожие вопросы
Предмет: Қазақ тiлi,
автор: мака15
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: НямкаНян
Предмет: Литература,
автор: Аноним