Question

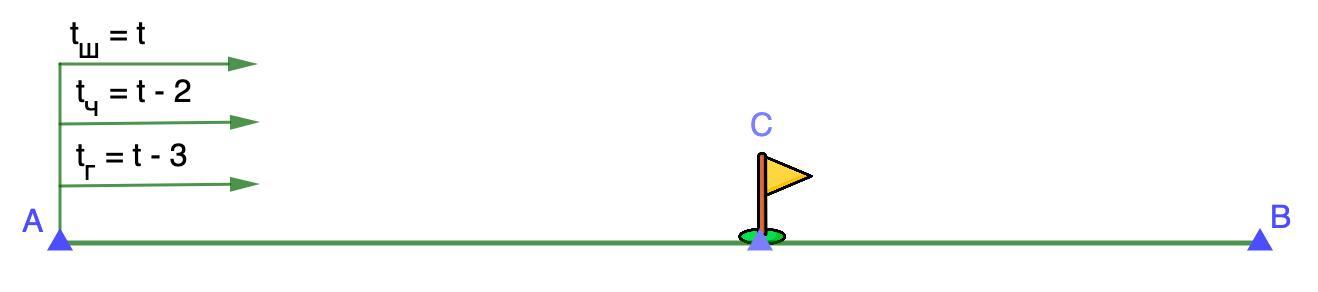
Из пункта `A` в пункт `B` вышла старуха Шапокляк. Через `2` часа после неё вышел Чебурашка, а ещё через час - крокодил Гена. Все трое шли с постоянной скоростью и без остановок. В какой-то момент времени все они оказались в одной точки дороги. На сколько минут раньше старухи Шапокляк прибыл в `B` Чебурашка, если известно, что старуха Шапокляк пришла ровно на полчаса позже крокодила Гены?

Answer 1

Ответ:

На 20 минут раньше старухи Шапокляк прибыл в B Чебурашка.

Пошаговое объяснение:

Найти, на сколько минут раньше старухи Шапокляк прибыл в B Чебурашка.

Из пункта A в пункт B вышла старуха Шапокляк. Через 2 часа после неё вышел Чебурашка, а ещё через час - крокодил Гена.

В какой-то момент времени все они оказались в одной точке дороги - С.

Пусть время  старухи Шапокляк - tч, тогда время Чебурашки - (t-2)ч, а время крокодила Гены - (t-3)ч.

До точки С все прошли одинаковое расстояние АС.

Вспомним:

$\displaystyle \boxed {S=vt;\;\;\;\;\;v=\frac{S}{t};\;\;\;\;\;t=\frac{S}{v}. }$

Знаем, что все трое прошли одинаковое расстояние АС, также знаем время каждого. Можем выразить их скорости:

Скорость старухи Шапокляк:

$\displaystyle v_1 = \frac{AC}{t}$   (км/ч)

Скорость Чебурашки:

$\displaystyle v_2 = \frac{AC}{t-2}$  (км/ч)

Скорость крокодила Гены:

$\displaystyle v_3 = \frac{AC}{t-3}$  (км/ч)

Далее рассмотрим путь на участке СВ.

Нам известно, что старуха Шапокляк пришла ровно на полчаса позже крокодила Гены.

Время старухи Шапокляк:

$\displaystyle t_1=\frac{CB\cdot{t}}{AC}$   (ч)

Время крокодила Гены:

$\displaystyle t_3=\frac{CB\cdot{(t-3)}}{AC}$   (ч)

Составим уравнение:

$\displaystyle t_1-t_3=\frac{1}{2} \\\\\\\frac{CB\cdot{t}}{AC}-\frac{CB\cdot{(t-3)}}{AC}=\frac{1}{2} \\\\2\cdot{CB}\cdot{t}-2\cdot{CB}\cdot{t}+6\cdot{CB}=AC\\\\6\;CB=AC\\\\\boxed {CB=\frac{AC}{6}}$

Тогда время на отрезке CB  старухи Шапокляк:

$\displaystyle t_1=\frac{CB\cdot{t}}{AC}=\frac{AC\cdot{t}}{AC\cdot6}=\frac{t}{6}$   (ч)

время Чебурашки:

$\displaystyle t_2=\frac{CB\cdot{(t-2)}}{AC}=\frac{AC\cdot{(t-2)}}{AC\cdot6}=\frac{t-2}{6} =\frac{t}{6}-\frac{1}{3}$   (ч)

Можем найти, на сколько минут раньше старухи Шапокляк прибыл в B Чебурашка:

$\displaystyle t_1-t_2=\frac{t}{6}- \frac{t}{6}+\frac{1}{3}=\frac{1}{3}$   (ч)

1ч = 60 мин

⇒ t₁ - t₂ = 20 мин

На 20 минут раньше старухи Шапокляк прибыл в B Чебурашка.