Предмет: Алгебра,
автор: oleksandrmaksimenko8
4 cos² x + 4cos x - 3 = 0
Приложения:
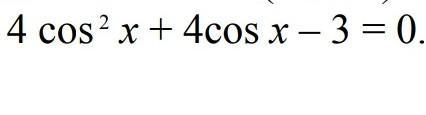
Ответы
Автор ответа:
0
Ответ:
х = ± , n ∈ Z.
Объяснение:
Внесем новую переменную z = сosx, тогда:
4z² + 4z - 3 = 0
D = 16 - 4 * 4 * (-3) = 64
cosx =
cosx = , нет корней, так как косинус принимает значения только от -1 до 1, тогда:
х = ± , n ∈ Z.
Похожие вопросы
Предмет: Русский язык,
автор: йцу89
Предмет: Русский язык,
автор: варя267
Предмет: Русский язык,
автор: Shule1111111
Предмет: Литература,
автор: zuhruk007
Предмет: Математика,
автор: channlethenortp7r70u