Предмет: Геометрия,
автор: ATASHOLL
1)прямая KE касается окружности с центром в точке О,K-точка касания.
Найдите OE,если КЕ=8см,а радиус окружности равен 6 см
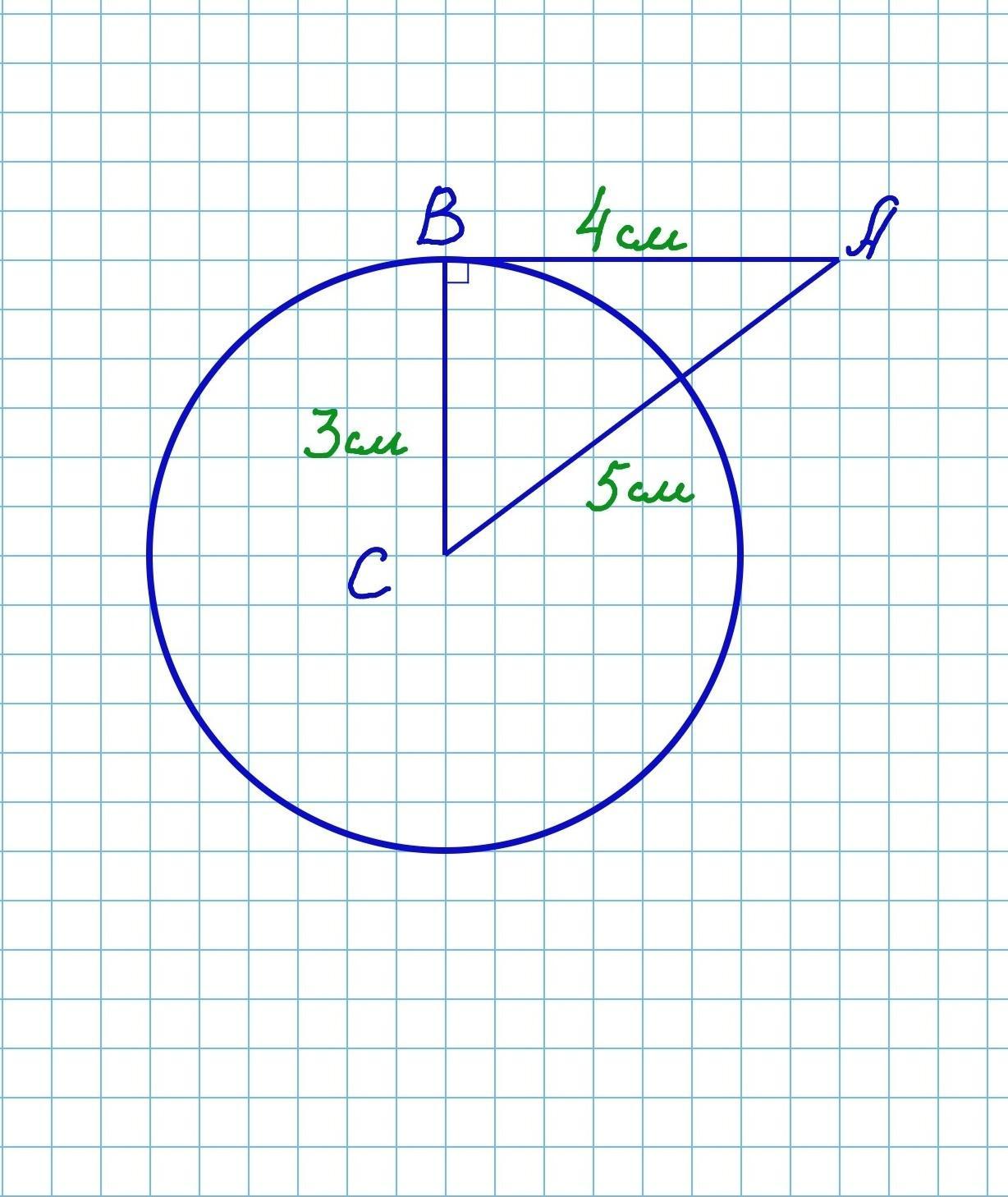
2)в треугольнике АВС,АВ=4см,ВС=3см,АС=5см.Докажите,что АВ-отрезок касательной,проведенной из точки А к окружности с центром в точке С и радиусом,равным 3см
РЕШИТЕ ТАК ЧТО БЫ БЫЛО ВСЕ РАСПИСАНО,ПРОШУУУУ
ДАЮ 40 БАЛЛОВ
Ответы
Автор ответа:
4
Ответ:
1) ОЕ равно 10см
Объяснение:
1) Дана окружность с центром в точке О. КЕ - касательная к окружности. КЕ=8см, радиус окружности R=6см. Найдём ОЕ.
Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.
- Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Проведём радиус КО в точку касания К. КЕ⟂КО. △ОКЕ - прямоугольный (∠К=90°).
По теореме Пифагора найдём гипотенузу ОЕ:
ОЕ²=КЕ²+КО²=8²+6²=64+36=100
ОЕ=10 см
2) Дан треугольник АВС. АВ=4см,ВС=3см,АС=5см. Окружность с центром в точке С и радиусом 3см.
Докажем, что отрезок АВ, проведенный из точки А к окружности является КАСАТЕЛЬНОЙ к окружности.
Рассмотрим треугольник АВС.
По теореме, обратной теореме Пифагора, он является прямоугольным, так как выполняется равенство:
АС²=ВС²+АВ²
5²=3²+4²
25=9+16
25=25
АС - гипотенуза. ∠В=90°. ВС и АВ - катеты. АВ⟂ВС.
Точка В лежит на окружности. Точка С - центр окружности. ВС - радиус окружности. ВС=3см. Таким образом отрезок АВ проходит через точку В, лежащую на окружности, и перпендикулярен радиусу ВС, проведенному в точку В.
Следовательно, по признаку касательной:
АВ является КАСАТЕЛЬНОЙ,проведенной из точки А к окружности с центром в точке С и радиусом,равным 3см.
Что и требовалось доказать.
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: odeo4ka
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: muratbek13
Предмет: Математика,
автор: arturron99