Предмет: Математика,
автор: ZABOR4EK
найдите cos a, если известно что sin =1/3 и а принадлежит 2 четверти
Ответы
Автор ответа:
0
Ответ:
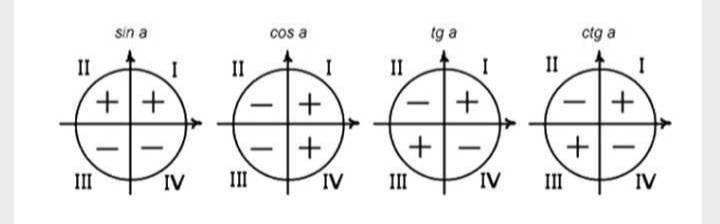
тк угол находится во второй четверти, то косинус его будет отрицательным <br />Соsа= -√1-(1/3)^2= -√1-1/9= -√8/√9= -2√2/3
Автор ответа:
8
Ответ:
Пошаговое объяснение:
выразим из основного тригонометрического тождества,
,подставляем:
так как косинус во второй четверти отрицательный (см.фото), то ответ:
Приложения:
ZABOR4EK:
спасибо
шикарно)
спасибо большое))))
Похожие вопросы
Предмет: Английский язык,
автор: Арсен170705
Предмет: Русский язык,
автор: ст99уп153
Предмет: Русский язык,
автор: vadimcherkavsk
Предмет: Алгебра,
автор: mmmonsterkill
Предмет: Русский язык,
автор: BADNM1528