Question

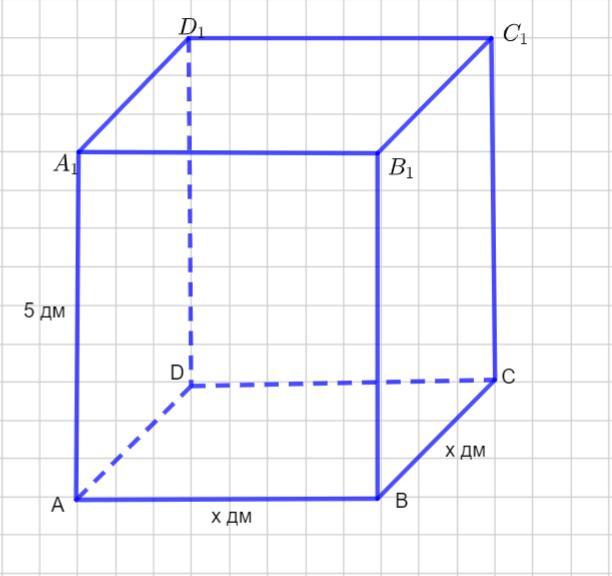
476. Найдите объем правильной четырехугольной призмы, которая имеет
высоту 5 дм и площадь полной поверхности 78 дм^2

Answer 1

Ответ:

Объем правильной четырехугольной призмы равен 45 дм³.

Пошаговое объяснение:

По условию задана правильная четырехугольная призма $ABCDA_{1} B_{1} C_{1} D_{1}$

Тогда в основании квадрат $ABCD$.

Пусть сторона квадрата будет х дм.

Площадь полной поверхности данной призмы равна сумме площади боковой поверхности и площадей двух оснований.

Если сторона квадрата равна х дм, то его площадь будет $S= x^{2}$  дм².

Площадь боковой поверхности призмы равна произведению периметра основания на высоту и в данном случае боковая поверхность будет равна $S= 4x\cdot 5 =20x$  дм²

Тогда полная поверхность будет равна

$S= 20x+2x^{2}$  дм²

По условию полная поверхность равна 78 дм².

тогда получим

$20x+2x^{2}=78|:2;\\x^{2} +10x=39;\\x^{2} +10x-39=0;\\D= 10^{2} -4\cdot1\cdot(-39)=100+156=256=16^{2} ;\\x{_1}= \dfrac{-10-16}{2} =-\dfrac{26}{2} =-13;\\\\x{_2}= \dfrac{-10+16}{2} =\dfrac{6}{2} =3$

Так как сторона квадрата не может быть выражена отрицательным числом, то х=3. Сторона основания правильной четырехугольной призмы равна 3 дм.

Найдем объем данной призмы как произведение площади основания на высоту

$V= a^{2} \cdot h;\\V= 3^{2} \cdot5=9\cdot 5 =45$

Тогда объем правильной четырехугольной призмы равен 45 дм³.