Question

на полуокружности CD взяты точки Fи Е так, что uCF = 102°, SED = 18°. Найди радиус полуокружности, если хорда EF равна 20 см. Решение: 1. Выполни соответствующий чертеж. 2. Найди градусную меру дуги FE > 3. Рассмотри ДFOE Усм. 4. Найди отрезок OF​

Answer 1

На полуокружности CD взяты точки Fи Е так, что U CF = 102°, U ED = 18°. Найди радиус полуокружности, если хорда EF равна 20 см.

Ответ:

Радиус окружности равен 20 см

Объяснение:

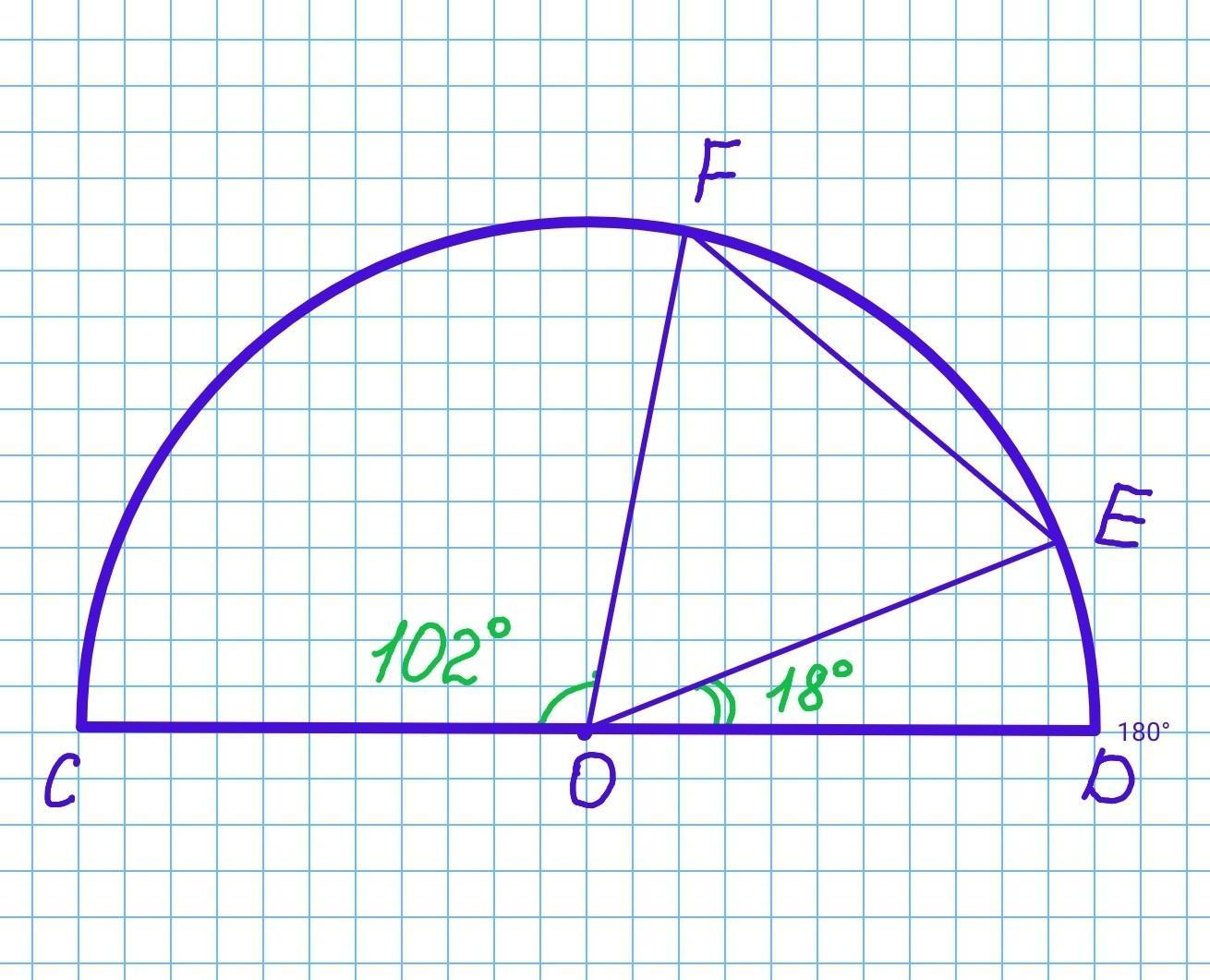
1. Выполним соответствующий чертеж по условию.

CD - полуокружность, следовательно U CD= 180°. ∠COD=180°.

• Если дуга окружности меньше полуокружности или является полуокружностью, то её градусная мера равна градусной мере соответствующего центрального угла.

U CF = 102°, следовательно центральный ∠COF=102°

U ED = 18°, следовательно центральный ∠DOE=18°.

В треугольнике FOE сторона EF является хордой. По условию EF=20см.

2. Найдём градусную меру дуги FE.

Центральный ∠FOE=∠COD-∠COF-∠DOE=180°-102°-18°=60°.

3. Рассмотрим △FOE.

СО=ОD=R, следовательно треугольник FOE - равнобедренный.

В равнобедренном треугольнике углы при основании равны:

∠F=∠E=(180°-∠FOE)/2=(180°-60°)/2=60°.

△FOE - равносторонний.

4. Найди отрезок OF.

Так как △FOE - равносторонний, то OF=OE=EF=20см.

Радиус окружности равен: R=OF=OE= 20см.