Question

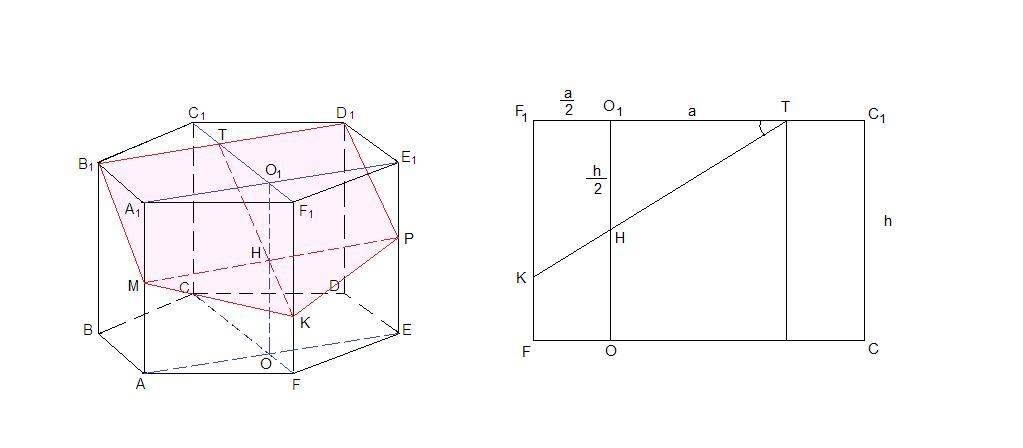
Точка M - середина ребра AA1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1


а) Докажите, что плоскость MB1D1 делит ребро FF1 в отношении 1 : 3.


б) Найдите угол между плоскостью основания призмы и плоскостью MB1D1, если AB = 5, AA1 = 10 корня из 3

Answer 1

Ответ:

а) FK : F₁K = 1 : 3 - доказано.

б) 60°

Объяснение:

а)

В правильной шестиугольной призме противоположные боковые грани параллельны.

М - середина АА₁.

Соединим точки B₁ и D₁, так как они находятся в одной грани.

B₁D₁ ∩ C₁F₁ = T.

Соединим точки В₁ и М, так как они находятся в одной грани.

Проведем D₁P. D₁P║В₁М, так как параллельные грани пересекаются секущей плоскостью по параллельным прямым,

• ∠В₁А₁М = ∠D₁E₁P = 90°,
• ∠А₁В₁М = ∠E₁D₁P как углы с соответственно параллельными сторонами,
• А₁В₁ = D₁E₁, значит ΔВ₁А₁М = ΔD₁E₁P по катету и прилежащему углу, тогда Р - середина ЕЕ₁.

D₁P = B₁M, D₁P║В₁М, тогда B₁D₁PM - параллелограмм и РМ║B₁D₁.

Плоскость (CC₁F₁) пересекает плоскость (АА₁Е₁) по прямой ОО₁.

МР пересекает ОО₁ в точке Н.  Так как ОО₁║АА₁, то Н - середина ОО₁.

Тогда секущая плоскость пересекает (CC₁F₁) по прямой ТН.

К - точка пересечения прямой ТН с ребром FF₁.

MB₁D₁PK - искомое сечение.

Надо доказать, что FK : F₁K = 1 : 3.

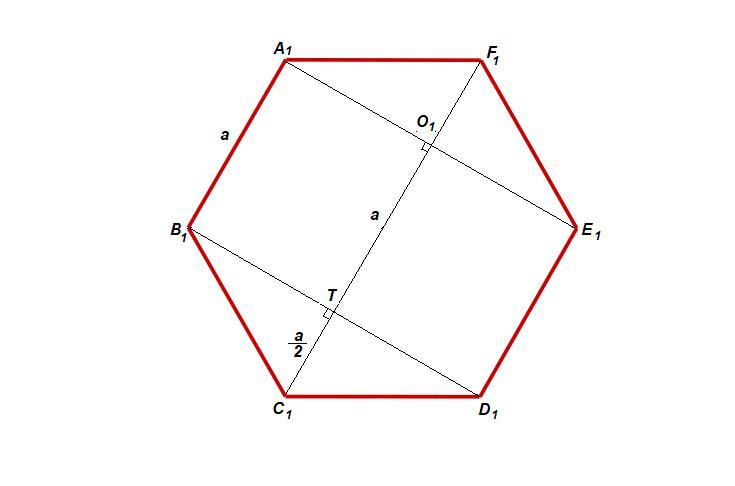
Несколько свойств правильного шестиугольника (рис. 2):

• большая диагональ в 2 раза больше стороны шестиугольника и параллельна сторанам, не имеющим с ней общих точек;
• меньшая диагональ перпендикулярна большей диагонали, если не имеет с ней общих вершин.

С₁В₁А₁F₁ - равнобедренная трапеция, А₁О₁ и В₁Т - ее высоты, тогда если А₁В₁ = а, то

C₁F₁ = 2а,    С₁Т = О₁F₁ = а/2

См. выносной чертеж на рис. 1:

ΔО₁ТН ~ ΔF₁TK по двум углам (прямоугольные и ∠Т общий), значит

$\dfrac{O_1H}{F_1K}=\dfrac{TO_1}{TF_1}$

Если боковое ребро h, то O₁H = 0,5h.

$\dfrac{0,5h}{F_1K}=\dfrac{a}{1,5a}$

$F_1K=\dfrac{0,5h\cdot 1,5a}{a}=0,75h=\dfrac{3}{4}h$

$FK=\dfrac{1}{4}h$

$\dfrac{FK}{F_1K}=\dfrac{1}{3}$

Что и требовалось доказать.

б)

Плоскости оснований призмы параллельны, поэтому найдем угол между секущей плоскостью и плоскостью верхнего основания.

C₁F₁ ⊥ B₁D₁ по свойству правильного шестиугольника,

TF₁ - проекция ТК на плоскость верхнего основания, значит

ТК⊥B₁D₁ по теореме о трех перпендикулярах.

∠F₁TK или иначе ∠О₁ТН - линейный угол угла между сечением и верхним основанием, искомый.

О₁Т = АВ = 5

О₁Н = 0,5 АА₁ = 0,5 · 10√3 = 5√3

$tg\angle O_1TH=\dfrac{O_1H}{O_1T}=\dfrac{5\sqrt{3}}{5}=\sqrt{3}$

∠O₁TH = 60°