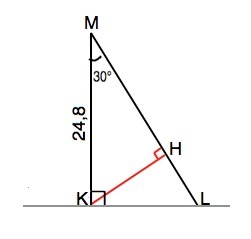
В треугольнике KLM отрезок KM = 24,8 дм , угол М = 30 градусов, угол К = 90 градусов. Найдите: 1)расстояние от точки К до прямой LM; 2)проекцию наклонной LM на прямой KL.
Ответы
1) Расстоянием от точки до прямой является длина отрезка, проведенного из этой точки перпендикулярно к данной прямой.
Для ∆ МKL этим расстоянием будет КН.
∆ МКН - прямоугольный, Катет КН противолежит углу 30°- по свойству такого катета равен половине гипотенузы треугольника КМН.
КН=МК:2=12,4 дм
2)
Вспомним:
Из точки вне какой либо прямой можно провести к ней множество прямых.
Из точки вне прямой можно провести к этой прямой только один перпендикуляр.
Прямая, пересекающая другую прямую и не перпендикулярная ей, называется наклонной.
Точка пересечения перпендикуляра с прямой и наклонной с прямой называется их основанием.
Отрезок, соединяющий основания наклонной и перпендикуляра, которые проведены из одной точки к одной и той же прямой, называется проекцией наклонной.
На рисунке приложения:
МК - перпендикуляр.
МL - наклонная.
КL - проекция наклонной на прямую KL.
Так как ∆ KML прямоугольный с острым углом М=30°, второй острый угол L=60°
Длину КL можно вычислить по т.Пифагора (приняв KL=x, ML=2x)
Другой способ:
КL=MK:tg60°=24,8/√3 дм
----------
Если очень коротко, без объяснений:
КН=КМ:2=12,4 (дм) ( по свойству катета против угла 30°)
КL=KM:tg60°=24,8/√3 (дм)