1. Накресліть різносторонній гострокутний трикутник.
1) Користуючись лінійкою зі шкалою та косинцем, знайдіть центр кола, описаного навколо даного трикутника.
2) Опишіть навколо трикутника коло.
2. Серединні перпендикуляри до сторін трикутника ABC перетинаються в точці O. Чи означає це, що:
а) OA = OB;
б) точка O може лежати на одній зі сторін трикутника?
3. Радіус описано¬го кола навколо прямокутного трикутника дорівнює 9дм. Знайдіть довжину гіпотенузи трикутника.
Ответы
Ответ:
1. См. рисунок
2. а) OA = OB = R
б) точка О может лежать на гипотенузе вписанного прямоугольного треугольника.
3. Длина гипотенузы треугольника равна 18 дм.
Объяснение:
1. Начертите разносторонний остроугольный треугольник.
1) используя линейку со шкалой и угольником, найдите центр круга, описанного вокруг данного треугольника.
2) опишите вокруг треугольника круг.
2. Серединные перпендикуляры к сторонам треугольника ABC пересекаются в точке O. Означает ли это, что:
а) OA = OB;
б) точка O может лежать на одной из сторон треугольника?
3. Радиус описанной окружности вокруг прямоугольного треугольника равен 9дм. Найдите длину гипотенузы треугольника.
- Центр описанной окружности около треугольника лежит на пересечении серединных перпендикуляров к сторонам треугольника.
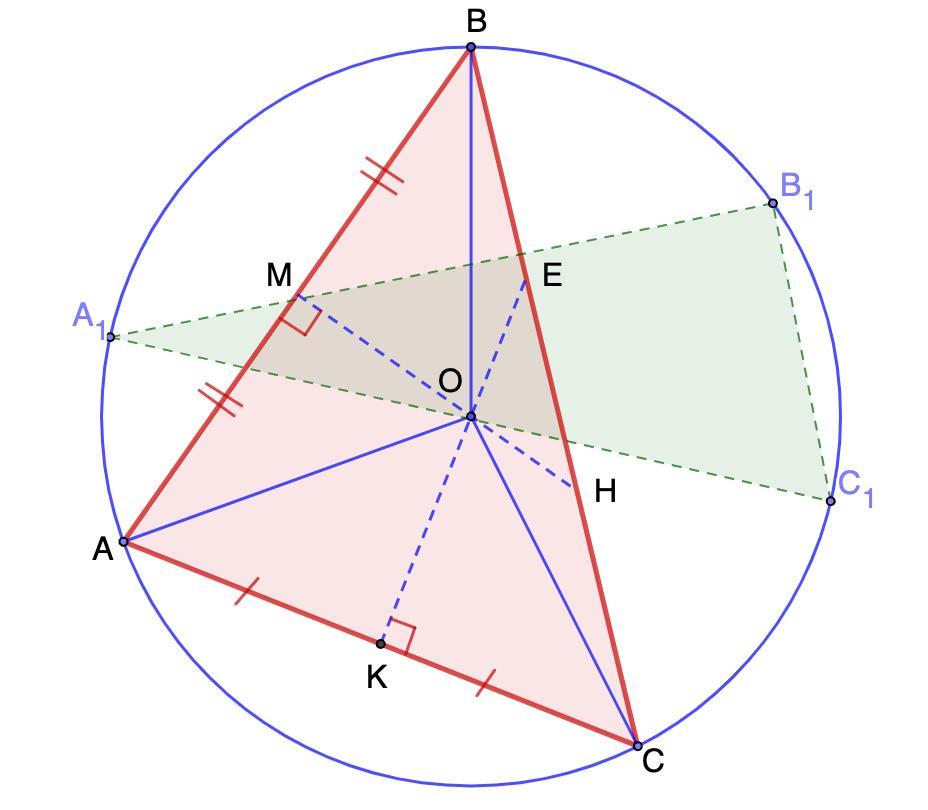
1.
Начертим остроугольный треугольник АВС.
1) Измерим стороны АВ и АС при помощи линейки со шкалой и отметим середины этих сторон - точки М и К соответственно.
С помощью угольника из точек М и К восстановим перпендикуляры МН и КЕ.
МН ∩ КЕ = О - центр описанной окружности.
2) Соединим О с вершинами ΔАВС.
ОА = ОВ = ОС = R - радиус описанной окружности.
Из центра О радиусом ОВ проведем окружность.
2.
a) Серединные перпендикуляры пересекаются в точке О.
О - центр описанной окружности.
⇒ OA = OB = R - радиусы описанной окружности.
б) Прямой вписанный угол опирается на диаметр.
⇒ точка О может лежать на гипотенузе вписанного прямоугольного треугольника.
3.
Радиус описанной окружности вокруг прямоугольного треугольника равен 9дм.
- Центр описанной окружности около прямоугольного треугольника лежит на его гипотенузе.
⇒ гипотенуза А₁С₁ является диаметром.
- Радиус равен половине диаметра.
⇒ А₁С₁ = 9дм · 2 = 18 дм.