Question

Обчисліть sin x, tg x, ctg x, якщо cos ax = -12/13.
π\2 < x < π

Answer 1

Ответ:

$\displaystyle sin(x)=\frac{5}{13}$ ; $\displaystyle tg(x) = -\frac{5}{12}$ ; $\displaystyle ctg(x) = -\frac{12}{5}$

Объяснение:

Дано: $\displaystyle cos(x)=-\frac{12}{13}$
$\displaystyle \frac{\pi }{2} < x < \pi$

Найти: sin(x), tg(x), ctg(x) - ?

Решение: 1) Т. к. $\displaystyle \frac{\pi }{2} < x < \pi$, то sin(x) будет положительным

Выделим sin(x) из основного тригонометрического тождества sin²(x)+cos²(x) = 1 : sin²(x) = 1-cos²(x); sin(x) = √(1-cos²(x))
$\displaystyle sin(x)=\sqrt{1-(-\frac{12}{13})^2 } =\sqrt{\frac{169-144}{169} } =\sqrt{\frac{25}{169} }=\frac{5}{13}$
2) tg(x) = sin(x)/cos(x)

$\displaystyle tg(x) = \frac{5}{13} :(-\frac{12}{13}) = \frac{5}{13} *(-\frac{13}{12}) = -\frac{5}{12}$
3) ctg(x) = (tg(x))⁻¹
$\displaystyle ctg(x) = (-\frac{5}{12})^{-1} = -\frac{12}{5} =-2\frac{2}{5} =-2,4$

Answer 2

Ответ:

• $\displaystyle sinx=\frac{5}{13} ;$
• $\displaystyle tgx=-\frac{5}{12};$
• $\displaystyle ctgx=-2\frac{2}{5}$

Объяснение:

• вычислим $sinx$, воспользовавшись основным тригонометрическим тождеством $sin^2\alpha+cos^2\alpha=1$ ( оно выполняется для любого $\alpha$ из промежутка  $0^\circ\leq \alpha\leq \pi$) :$\displaystyle sin^2x+cos^2x=1;\\sin^2x+\bigg(-\frac{12}{13} \bigg)^2=1;\\sin^2x+\frac{144}{169} =1;\\sin^2x=1-\frac{144}{169} =\frac{169}{169} -\frac{144}{169} =\frac{25}{169} ;\\sinx=\pm\sqrt{\frac{25}{169} } =\pm\frac{5}{13}$  
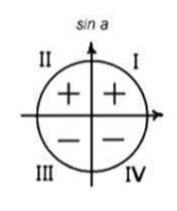
• по условию  $\displaystyle\frac{\pi }{2} < x < \pi$, т.е. $\displaystyle x\in\bigg(\frac{\pi }{2} ;\pi \bigg)\in(90^\circ;180^\circ)$, а в этих четвертях синус положительный (см. фото), то оставляем только одно значение: $sinx=\frac{5}{13}$.
• вычислим $tgx$ по формуле $\displaystyle tg\alpha=\frac{sin\alpha}{cos\alpha}$: $\displaystyle tgx=\frac{sinx}{cosx} =\frac{\frac{5}{13} }{-\frac{12}{13} } =\frac{5}{\not13} \cdot \bigg(-\frac{\not13}{12} \bigg)=-\frac{5}{12}$
• $ctgx$-величина,обратная $tgx$, иными словами,$\displaystyle ctgx=\frac{1}{tgx} =\frac{cosx}{sinx}=\frac{1}{-\frac{5}{12} }=\frac{-\frac{12}{13} }{\frac{5}{13} } =-\frac{12}{\not13} \cdot\frac{\not13}{5} =-\frac{12}{5} =-2\frac{2}{5}$