Предмет: Математика,
автор: DENNIS2445
Решите пожалуйста пример. Границя функций в точке.
10 пример все остальные не нужно.
Заранее спасибо.
Приложения:
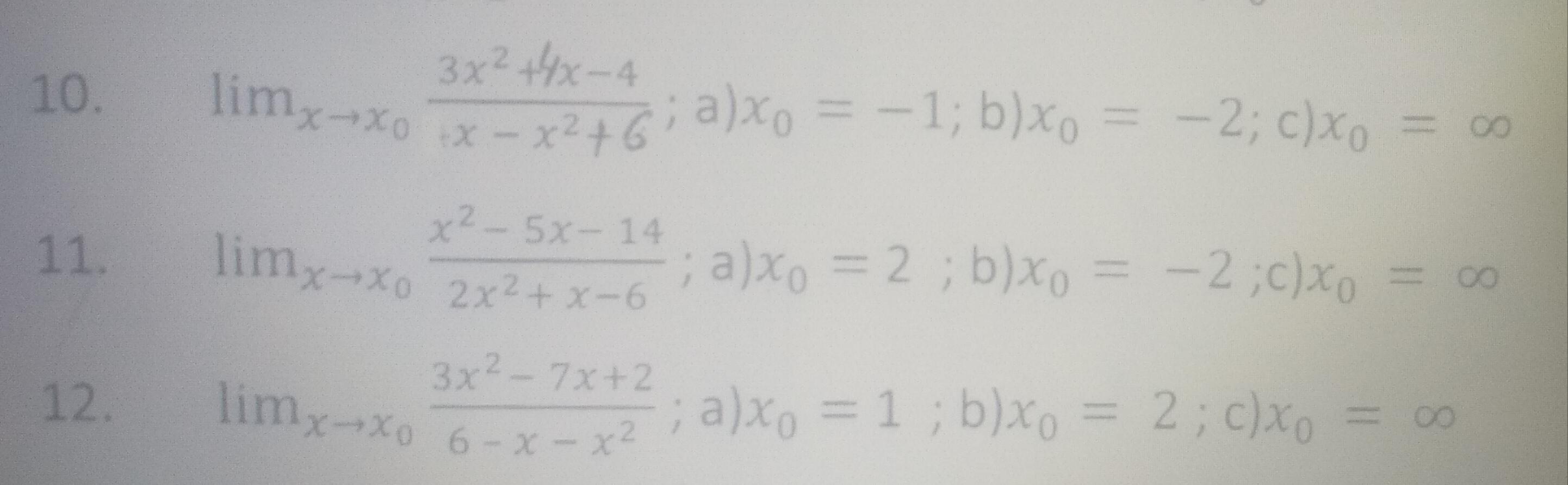
Ответы
Автор ответа:
1
Ответ:
а)
б)
в) ∞
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Elvira11121989
Предмет: Окружающий мир,
автор: Натусик91
Предмет: Русский язык,
автор: LEDO1
Предмет: Химия,
автор: HanterXX
Предмет: Математика,
автор: gdfgdfhfgdhf