Предмет: Математика,
автор: YSLmurda
В основании прямой призмы лежит квадрат с диагональю  . Найди площадь боковой поверхности призмы, если её высота равна
. Найди площадь боковой поверхности призмы, если её высота равна 
Ответы
Автор ответа:
1
Sбок=Росн*h
В основании квадрат , сторона х
х²+х²=(3√14)²
2х²=9*14
х²=9*7 → х=3√7 → Росн=4*3√7=12√7
Sбок=12√7*8√7=12*8*7=672
Автор ответа:
0
Ответ:
672
Пошаговое объяснение:
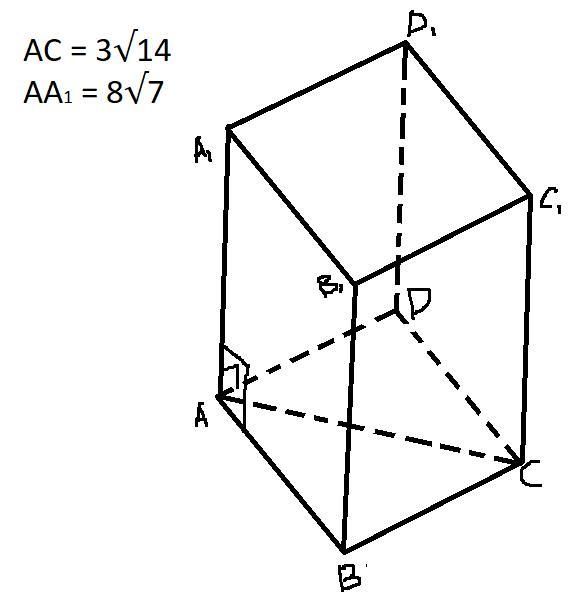
Пусть дана призма ABCDA1B1C1D1 (см. рис.), где AC = 3√14, AA1 = 8√7.
Найдём стороны основания. По т. Пифагора
Так как призма прямая с основанием в виде квадрата, площадь её боковой поверхности: , где h - высота, a - сторона основания. h = AA1 = 8√7, a = AD = 3√7
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Ал4сей
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Hasmik15
Предмет: Русский язык,
автор: yYAROSLAVv