Предмет: Математика,
автор: kolobok9805
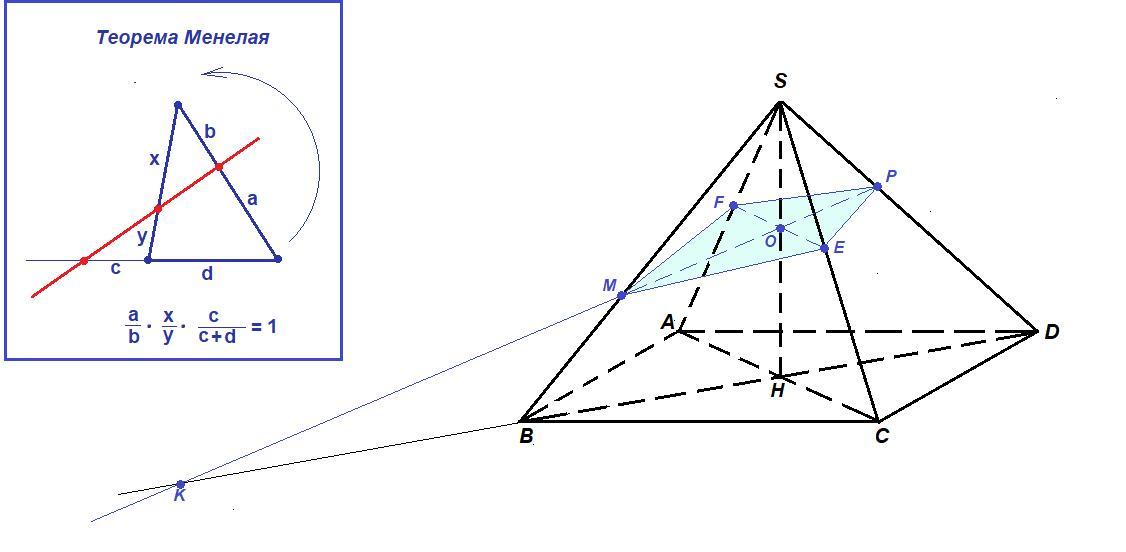
Основание четырехугольной пирамиды SABCD – параллелограмм ABCD. На ребрах SB и SD соответственно взяты точки M и P так, что BS=3BM, SD=3SP. Через эти точки проведена плоскость, параллельная AC. Постройте сечение пирамиды этой плоскостью и определите в каком отношении оно делит ребро SC.
Ответы
Автор ответа:
6
Ответ:
SE : EC = 4 : 5
Пошаговое объяснение:
Построение сечения:
- Проведем отрезок МР. Так как МР и SН лежат в одной плоскости (BSD), то они пересекаются в точке О.
- Через точку О в плоскости (ASC) проведем прямую, параллельную АС. Она пересечет ребро SA в точке F и ребро SC в точке Е.
- Соединим точки Р и М с точками F и Е.
- Сечение PFME проходит через точки Р и М и параллельно АС, так как в нем лежит прямая FE, параллельная АС, значит
- PFME - искомое сечение.
Пусть К - точка пересечения прямых РМ и BD.
Для треугольника BSD и секущей РК применим теорему Менелая:
По условию BS = 3BM, значит ВМ - одна часть, а BS - 3 таких части.
SM = BS - BM, то есть SM - 2 таких части. Тогда
Аналогично,
Подставляем эти отношения:
⇒
Выразим HK как часть KD:
,
Теперь для треугольника DSH и секущей РК применим теорему Менелая:
Так как ОЕ║АС, то по обобщенной теореме Флеса
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: LukeKast
Предмет: Русский язык,
автор: лмпшмсоли
Предмет: Українська мова,
автор: катя34а
Предмет: Математика,
автор: Serdolina78
Предмет: Русский язык,
автор: twitder