Предмет: Алгебра,
автор: alinakysloglad
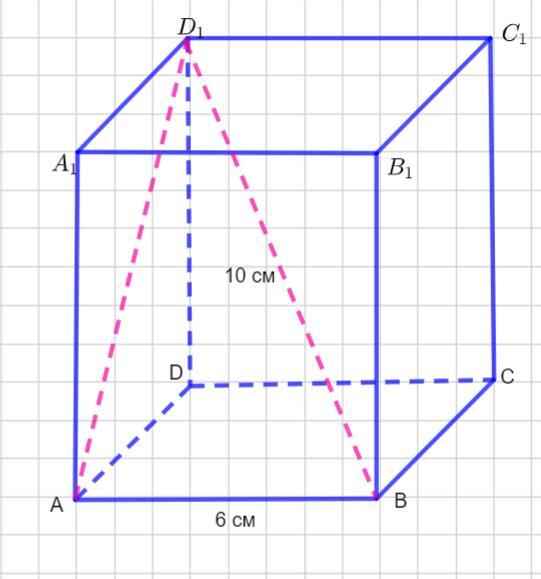
Знайдіть діагональ бічної грані правильної чотирикутної призми якщо сторона її основи дорівнює 6 см а діагональ призми 10 см
Ответы
Автор ответа:
5
Ответ:
Диагональ боковой грани равна 8 см.
Объяснение:
Пусть дана правильная четырехугольная призма
Тогда в основании квадрат со стороной 6 см.
Рассмотрим Δ. Так как
- квадрат, то DA⊥ AB.
По теореме о трех перпендикулярах ⊥ AB.
Тогда Δ - прямоугольный с гипотенузой
cм и катетом АВ =6 см.
Найдем другой катет по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Тогда диагональ боковой грани равна 8 см.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: R0sie
Предмет: Английский язык,
автор: Lina000007
Предмет: Русский язык,
автор: yfainberg
Предмет: Химия,
автор: mditennis
Предмет: Русский язык,
автор: nata838363