Question

Вычислить площадь плоской фигуры, ограниченной линиями:

y=x^2-x, y=2x
ОТВЕТ НУЖЕН РАЗВЁРНУТЫЙ

Answer 1

Ответ:

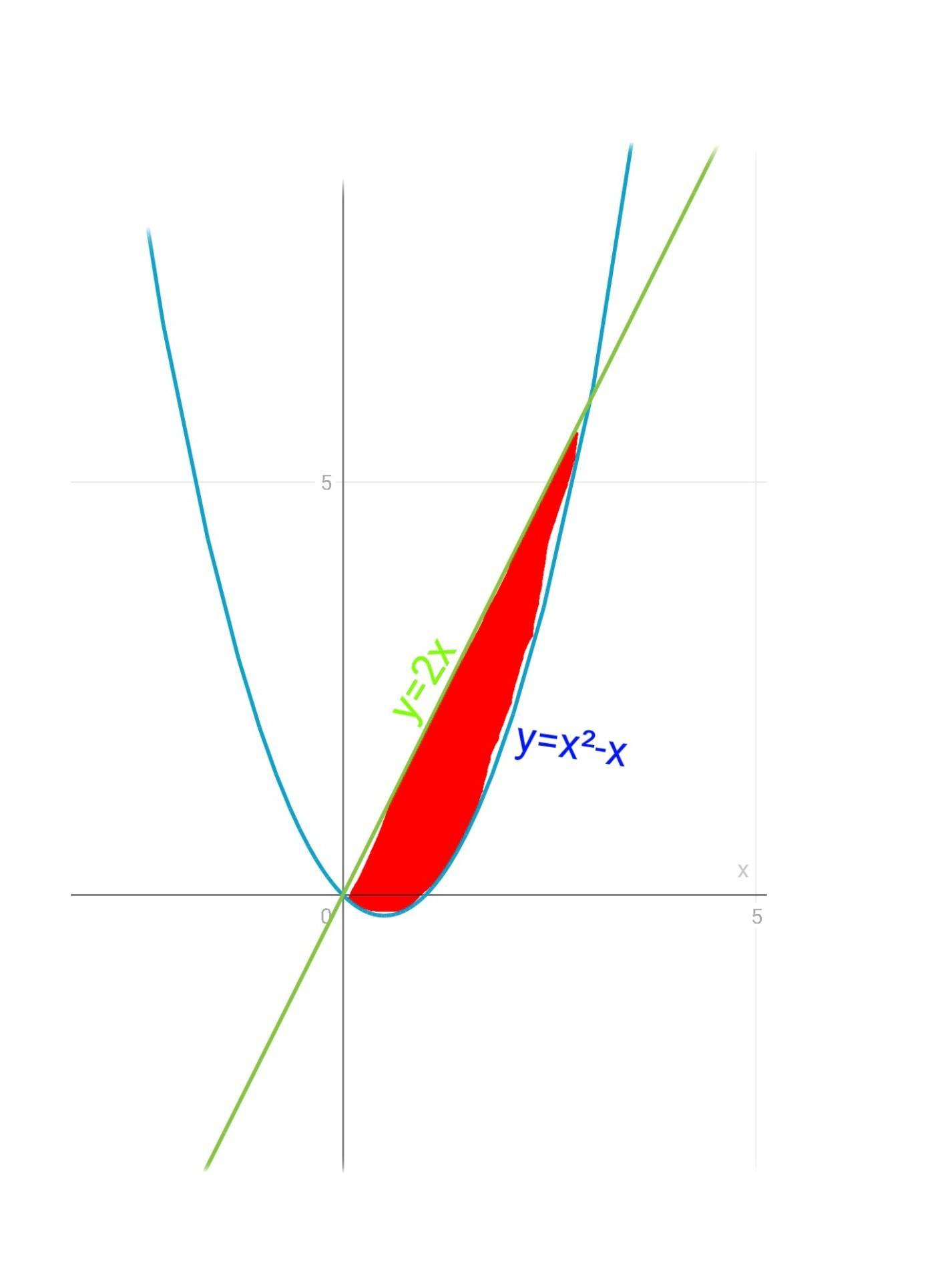
Нужно найти площадь закрашенной части.

Найдем точки пересечения, для этого приравняем функции:

${x}^{2} - x = 2x \\ {x}^{2} - x - 2x = 0 \\ {x}^{2} - 3x = 0 \\ x(x - 3) = 0 \\ x_{1} = 0 \: \: \: \: \: \: \: \: \: \: x - 3 = 0 \\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: x_{2} = 3$

Эти точки пересечения будут нашими отрезками в интегрировании.

В графике в закрашенной части сверху прямая y=2x, а снизу парабола y=x²-x, поэтому в интегрировании отнимем x²-x от 2x.

$\int_{0}^{3} 2x - ( {x}^{2} - x)dx = \int_{0}^{3} 2x - {x}^{2} + xdx = \\ \int_{0}^{3} - {x}^{2} + 3xdx =( - \frac{ {x}^{3} }{3} + 3 \times \frac{ {x}^{2} }{2} )| _{0}^{3} = \\ - \frac{ {3}^{3} }{3} + \frac{3 \times {3}^{2} }{2} - ( - \frac{ {0}^{3} }{3} + \frac{3 \times {0}^{2} }{2} ) = \\ - \frac{27}{3} + \frac{27}{2} - (0 + 0) = - 9 + 13.5 = 4.5$

Ответ: 4,5 квадратных единиц.

Запишу формулу интеграла, которой мы пользовались:

$\int a {x}^{n} dx = a \times \frac{ {x}^{n + 1} }{n + 1} + c$