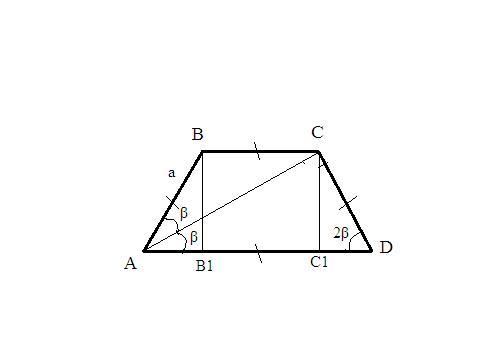
Рис. 618 Дано ABCD трапеция, угол BAC = бета
Найти: AD

Ответы
по условию диагональ АС - биссектриса ∠ВАD. Тогда ΔАВС - равнобедренный (∠ САD =∠ACВ=β - внутренние накрест лежащие при параллельных прямых ВС и AD и секущей АС).
значит. ВС=АВ=CD=а, опустим из вершины С высоту на большую сторону АD, пусть это будет СК.
ΔАСD разбился на два прямоугольных треугольника АСК и DСК, чтобы найти АD. надо знать АК и КD,
чтобы найти АК, надо знать АС, найдем АС из ΔАВС по теореме косинусов, АС²=АВ²+ВС²-2АВ*ВС*cos∠АВС; ∠АВС=180-2β;
АС²=а²+а²-2а*а*cos(180-2β)=2а²+2а²cos(2β)=2а²*(1+cos(2β))=
2а²*(2cos²(β))=4а²cos²(β), ∠ ВАD=2β- острый⇒
АС=2а*cos(β);
т.о., АК=АС*cosβ=2acos²(β);
из ΔСКD:KD=CD*cos(2β); KD=а*cos(2β);
АD= АК+КD=2acos²(β)+а*cos(2β).
Ответ:
Объяснение:
АС диагональ и биссектриса в равнобедренной трапеции ∠ВАС=β, ∠BAD=∠ADC=2β;
по свойству секущей ∠ВАС=∠ВСА=β ⇒ АВ=ВС;
опускаем перпендикуляры ВВ1 и СС1;
AD=AB1+B1C1+C1D; B1C1=BC=a; AB1=C1D;
ΔCC1D прямоугольный, ∠ C1DC=2β ⇒ C1D=CD*cos(2β)=acos(2β);
AD=2acos(2β)+a.