Question

Очень срочно, завтра зачет :с Помогите пожалуйста :*
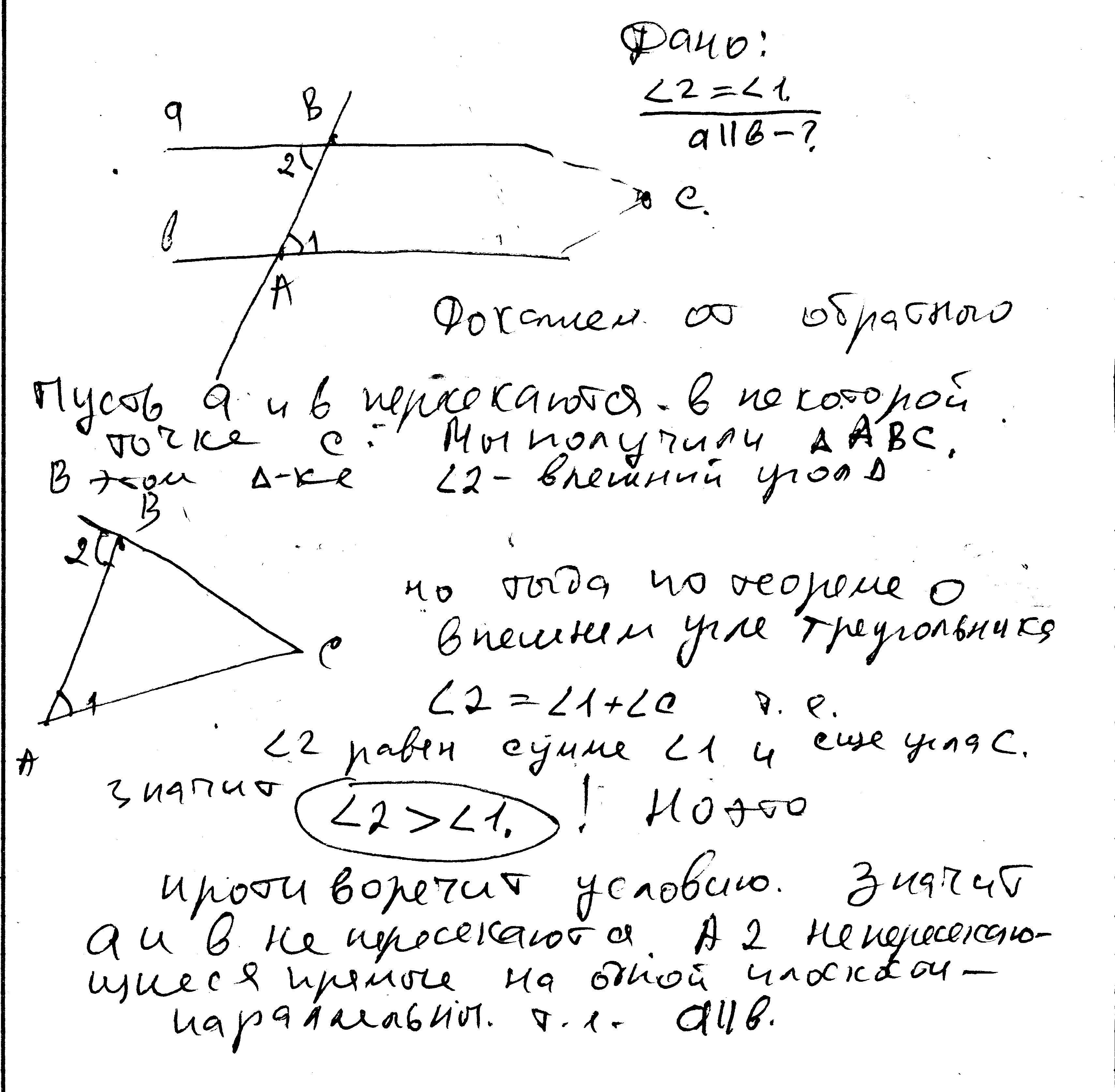
1.Докажите, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.;
2.Объясните, какие утверждения называются аксиомами.
Приведите примеры аксиом;
3.Сформулируйте аксиому параллельных прямых.
^^

Answer 1

1. Ответ на первый в скане.
2. Аксиома - математическое предложение, принимаемое без доказательства. В основе геометрии, (а по сути любой естественной науки)  лежат несколько аксиом, которые приняли без доказательства, так как доказательство невозможно и они кажутся очевидными. Например, аксиома о том, что параллельные прямые не пересекаются в евклидовой геометрии лежит в основе той геометрии, которую мы изучаем в школе. 2 человека засомневались в верности этой аксиомы. Отказались от этой аксиомы и приняли аксиому, что параллельные прямые пересекаются. И построили свои геометрии, в которые евклидова входит как частный случай. Эти люди Лобачевский и Риман. Теперь есть кроме евклидовой еще геометрия Лобачевского и риманова геометрия. Вот такое дело аксиомы.
3. Аксиома параллельных прямых:
 Через любую точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.
Но вариантов формулировки этой аксиомы видимо-невидимо.