Предмет: Геометрия,
автор: jala1903
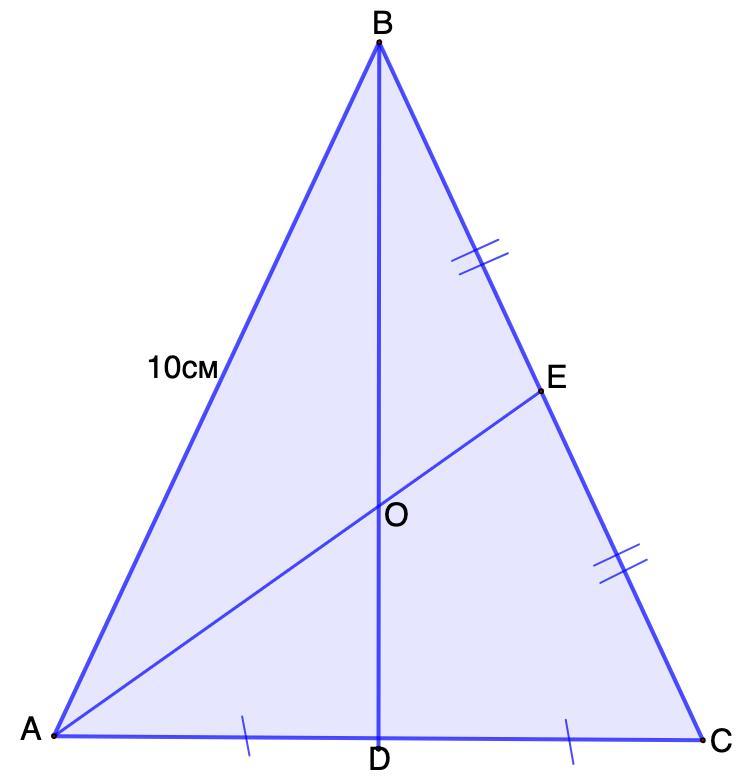
В треугольнике ABC, AB=≈BC, AE и BD медианы, АВ=10 см и
AD-OD=(3 1/3см). Найдите OD
Ответы
Автор ответа:
1
Ответ:
OD = 2 2/3 см.
Объяснение:
Требуется найти ОD.
Дано: ΔАВС.
АВ = ВС;
АЕ и ВD - медианы;
АЕ ∩ ВD = О
AD - OD = 3 1/3 см
Найти: OD
Решение:
1. Рассмотрим ΔАВС - равнобедренный.
- В равнобедренном треугольнике медиана, проведенная к основанию, является высотой.
⇒ BD ⊥ AC.
- Медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины.
⇒ BD = 3 · OD
2. Рассмотрим ΔАВD - прямоугольный.
AD - OD = 3 1/3 см ⇒ OD = (AD - 3 1/3) см.
Пусть AD = х см, тогда OD = (x - 3 1/3) см,
⇒ BD = 3 · (x - 3 1/3) = (3x - 10) (см)
По теореме Пифагора:
АВ² = AD² + BD²
100 = x² + 9x² - 60x + 100
10x (x - 6) = 0
x₁ = 0 - не подходит
х₂ = 6
AD = 6 см
⇒ OD = (AD - 3 1/3) = 6 - 3 1/3 = 2 2/3 (см).
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: ПростоЧелдобрек
Предмет: Русский язык,
автор: каусар5
Предмет: Русский язык,
автор: Ботик228
Предмет: Русский язык,
автор: 20kosmos32
Предмет: Математика,
автор: varvarauhimenko