Question

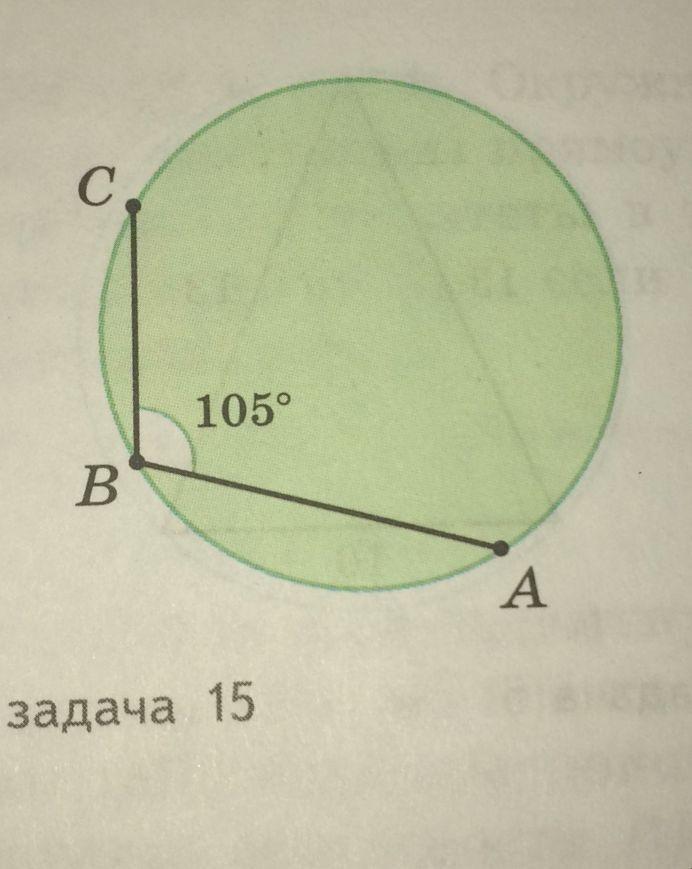
из одной точки окружности проведены 2 хорды угол между которыми равен 105°. найдите отношение этих длин этих хорд если одна из них равна радиусу этой окружности

Answer 1

Ответ:

Отношение этих длин хорд равно √2 : 1

Объяснение:

Требуется найти отношение этих длин хорд, если одна из них равна радиусу этой окружности.

Дано: Окр.(О,R)

ВС и АВ - хорды;

∠АВС = 105°

ВС = R

Найти: АВ : ВС

Решение:

В точки А, В, С проведем радиусы.

1. Рассмотрим ΔОВС.

ВС = ОС = ОВ = R (условие)

⇒ ΔОВС - равносторонний.

• В равностороннем треугольние все углы равны и их градусная мера составляет 60°.

⇒ ∠СВО = 60°

2. Рассмотрим ΔВОА.

ВО = ОА = R

⇒ ΔВОА - равнобедренный.

∠ОВА = ∠АВС - ∠СВО = 105° - 60° = 45°

• Углы при основании равнобедренного треугольника равны.

⇒ ∠ОАВ = 45°.

• Сумма углов треугольника равна 180°.

⇒ ∠ВОА = 180° - (45° + 45°) = 90°

ΔВОА - равнобедренный, прямоугольный.

По теореме Пифагора:

АВ² = ВО² + ОА² = R² + R²

АВ = R√2

3. AB : BC = R√2 : R = √2 : 1

Отношение этих длин хорд равно √2 : 1.