Предмет: Геометрия,
автор: artemon853
5. Використовуючи рисунок, доведіть, що точка, яка лежить на бісектрисі
кута АOB, розташована на однаковій відстані від прямих AO і BO.
Приложения:
Ответы
Автор ответа:
1
Объяснение:
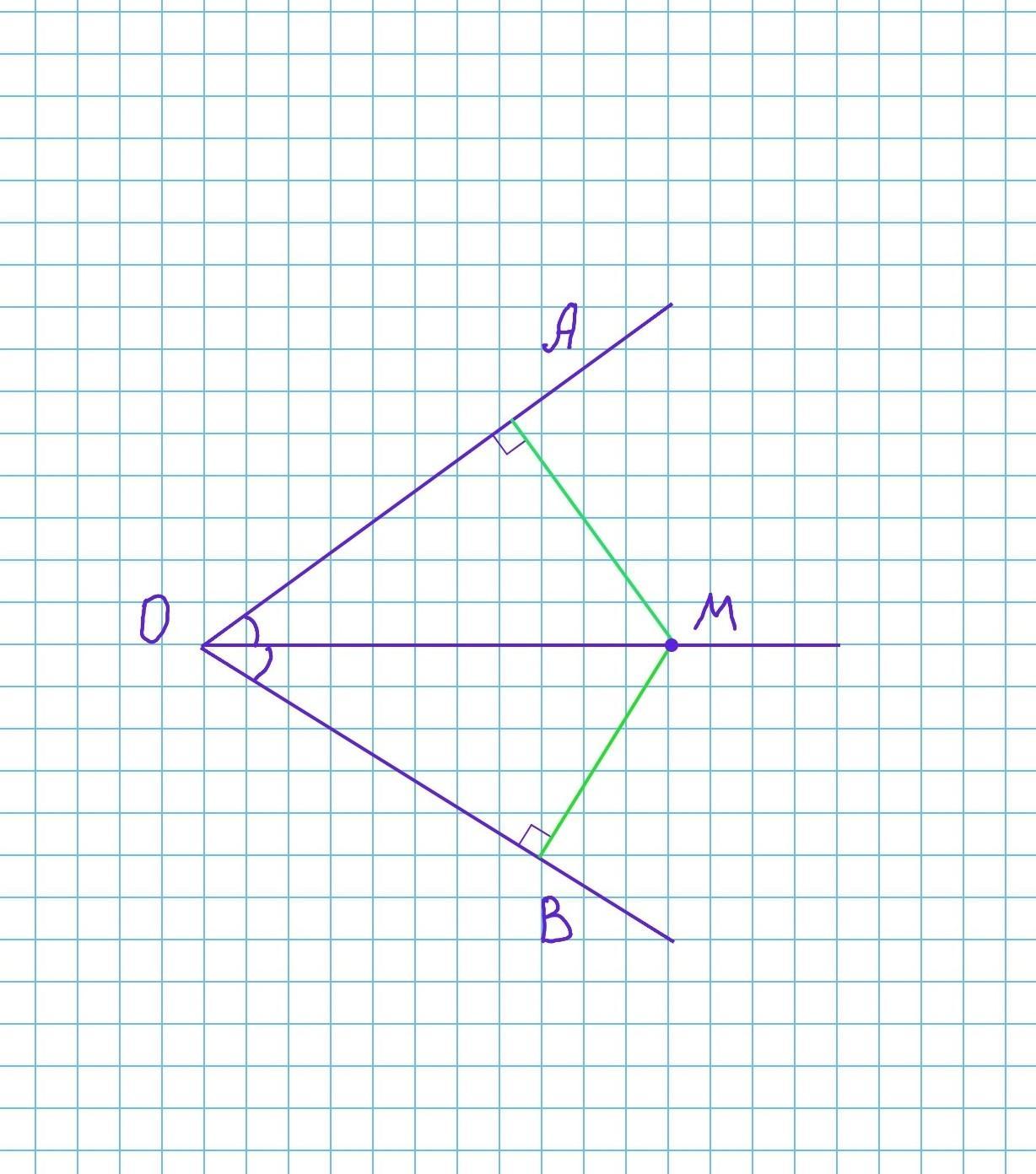
Дано: ∠АОВ, ОМ - бісектриса кута АОВ. Точка М ∈ ОМ
Довести: АМ=ВМ
- Відстанню від точки до прямої називають довжину перпендикуляра, проведеного з даної точки до даної прямої.
МА⟂АО, МА - відстань від точки М до прямої АО.
МВ⟂ВО, МВ - відстань від точки М до прямої ВО.
Розглянемо △АОМ і △ВОМ.
∠АОМ=∠ВОМ, так як ОМ - бісектриса кута АОВ,
∠ОАМ=∠ОВМ=90°,
ОМ - спільна сторона.
△АОМ = △ВОМ за гіпотенузою і гострим кутом.
З рівності трикутників слідує рівність катетів: АМ=ВМ, що і треба довести.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Ali0802
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: АлисаТрубина2
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: makssurikov230