Question

Найдите площадь равнобедренного треугольника,если высота опущенная из вершины прямого угла этого прямоугольного треугольника равна 6√2 ​

Answer 1

Ответ:

Объяснение:

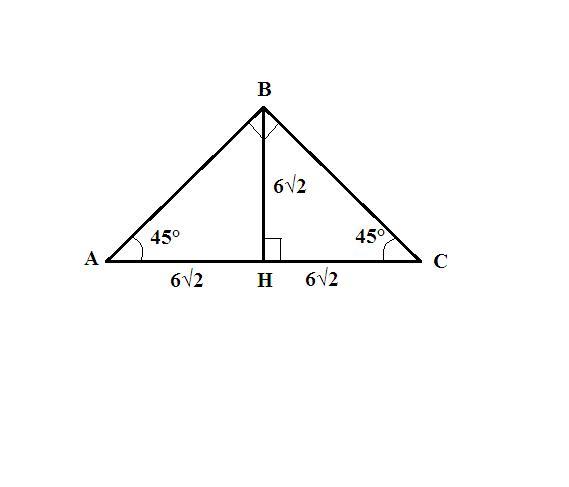
ΔАВС равнобедренный и прямоугольный ⇒ гипотенуза треугольника АС - основание, боковые стороны АВ и ВС - катеты. Углы при основании равнобедренного треугольника равны ⇒ ∠А=∠С= 90/2=45°. Высота ВН равная 6√2, проведенная из вершины, является медианой. Треугольники, образованные высотой, половиной основания и боковой стороной, прямоугольные и равнобедренные. катеты ВН и НС - 6√2. Тогда основание исходного треугольника АС - 2*6√2=12√2, а высота, проведенная к ней ВН - 6√2 (по условию). Площадь - 12√2*6√2/2=12*6=72 ед².