Предмет: Алгебра,
автор: Аноним
Помогите сделать алгебру, пожалуйста
Приложения:
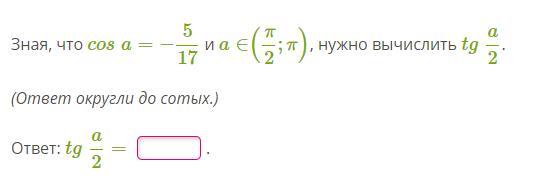
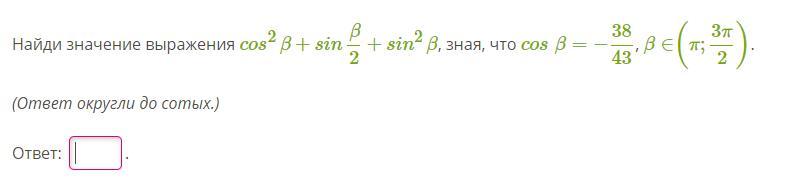

Ответы
Автор ответа:
2
Ответ:
Используем формулы половинного аргумента:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: помогитеумоляю13452
Предмет: Русский язык,
автор: danil884
Предмет: Русский язык,
автор: Katerina240404
Предмет: Математика,
автор: gulnareisayeva
Предмет: Математика,
автор: makar11k