Предмет: Математика,
автор: skezzoffmasked
Обчислисти |5a + 3b| якщо |a|=2, |b|=4? і кут між векторами 120градусів
Приложения:
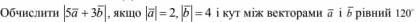
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: AlinaSannnnnnna
Предмет: Беларуская мова,
автор: vasilevicheduard
Предмет: Русский язык,
автор: алинка429
Предмет: Физика,
автор: cristalik51
Предмет: Алгебра,
автор: kikakokaka