Предмет: Алгебра,
автор: velmasa180
Срочнооо!!!!очень нужно
Приложения:
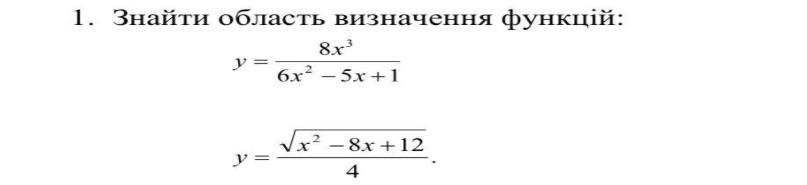
Ответы
Автор ответа:
0
Ответ:
1.
2.
Объяснение:
Требуется найти область определения функций.
1.
- На ноль делить нельзя.
⇒ 6х² - 5х + 1 ≠ 0
Найдем корни:
⇒
2.
- Подкоренное выражение неотрицательно.
⇒
х² - 8х + 12 ≥ 0
Найдем корни:
Получили:
(х - 6)(х - 2) ≥ 0
Решим методов интервалов:
Похожие вопросы
Предмет: Русский язык,
автор: kristinasol158
Предмет: Английский язык,
автор: Nik1451
Предмет: Другие предметы,
автор: pavlenkodiana39
Предмет: Математика,
автор: hhhjhjltschwdged
Предмет: Биология,
автор: ARON20052005