Question

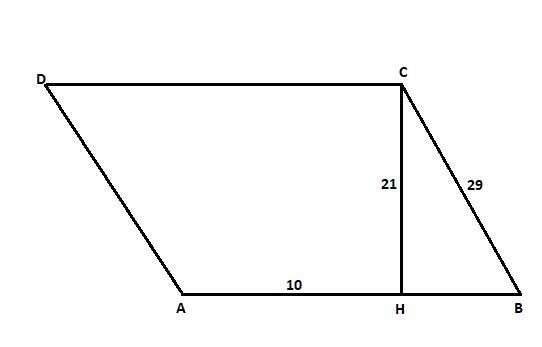
Дан параллелограмм АВСD в котором высота СН делит сторону АВ на отрезки АН - 10 и ВН. Сторона ВС - 29 а высота СН 21. Найдите площадь параллелограмма​

Answer 1

Ответ:

630 кв.см.

Объяснение:

Дан параллелограмм АВСD в котором высота СН делит сторону АВ на отрезки АН = 10 см и ВН.

Сторона ВС = 29 см, а высота СН = 21 см.

Найдите площадь параллелограмма​.

Решение:

Смотрите рисунок.

Треугольник BCH - прямоугольный. По теореме Пифагора:

BH^2 = BC^2 - CH^2 = 29^2 - 21^2 = 841 - 441 = 400

BH = √400 = 20 см

AB = AH + BH = 10 + 20 = 30 см

Площадь параллелограмма равна произведению основания на высоту.

S(ABCD) = AB*CH = 30*21 = 630 кв.см.